Um Toleranzgrenzen nach ISO 16269 zu berechnen, gehen wir schrittweise vor:
- Datensammlung: Stellen Sie sicher, dass Sie eine ausreichende Anzahl von Messungen haben. Die Stichprobengröße sollte mindestens 30 betragen.
- Normalverteilung prüfen: Die Daten sollten annähernd normalverteilt sein. Dies können Sie mit statistischen Tests wie dem Shapiro-Wilk-Test überprüfen.
- Mittelwert und Standardabweichung berechnen: Ermitteln Sie den Mittelwert (x̄) und die Standardabweichung (s) Ihrer Stichprobe.
- Toleranzfaktor bestimmen: Wählen Sie den passenden Toleranzfaktor (k) aus den Tabellen der ISO 16269. Dieser hängt von der Stichprobengröße, dem gewünschten Konfidenzniveau und dem Anteil der Population ab, der innerhalb der Grenzen liegen soll.
- Toleranzgrenzen berechnen:
- Obere Toleranzgrenze: UTL = x̄ + k * s
- Untere Toleranzgrenze: LTL = x̄ – k * s
Die entsprechenden k Werte kannst Du in folgendem online Tool berechnen.
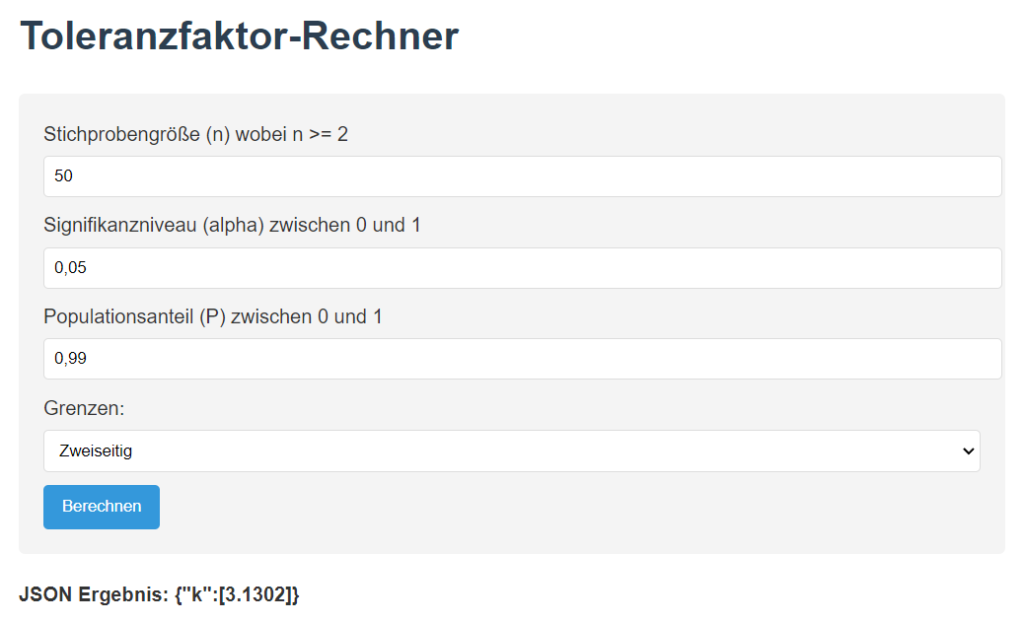
Die ISO 16269 befasst sich mit der statistischen Interpretation von Daten. Teil 6 dieser Norm, ISO 16269-6, befasst sich speziell mit der Bestimmung statistischer Toleranzintervalle.
Ein statistisches Toleranzintervall ist ein geschätztes Intervall, das auf einer Stichprobe basiert und mit einer bestimmten Konfidenzstufe (z. B. 0,95) mindestens einen bestimmten Anteil p der Elemente der Grundgesamtheit enthält.
Die Grenzen eines statistischen Toleranzintervalls werden als statistische Toleranzgrenzen bezeichnet.
Die Konfidenzstufe 1 − α ist die Wahrscheinlichkeit, dass ein auf die vorgeschriebene Weise konstruiertes statistisches Toleranzintervall mindestens einen Anteil p der Grundgesamtheit enthält.2 Umgekehrt ist die Wahrscheinlichkeit, dass dieses Intervall weniger als den Anteil p der Grundgesamtheit enthält, gleich α.2
In der Norm ISO 16269-6 werden sowohl einseitige als auch zweiseitige statistische Toleranzintervalle beschrieben.
Ein einseitiges Intervall wird mit einer oberen oder einer unteren Grenze konstruiert, während ein zweiseitiges Intervall sowohl mit einer oberen als auch mit einer unteren Grenze konstruiert wird.2
Zwei Arten von statistischen Toleranzintervallen werden in ISO 16269-6 behandelt: parametrische und verteilungsfreie.
Der parametrische Ansatz basiert auf der Annahme, dass das in der Grundgesamtheit untersuchte Merkmal normalverteilt ist. Daher kann die Konfidenz, dass das berechnete statistische Toleranzintervall mindestens einen Anteil p der Grundgesamtheit enthält, nur dann mit 1 − α angenommen werden, wenn die Normalverteilungsannahme zutrifft.
Für normalverteilte Merkmale wird das statistische Toleranzintervall mit einer der in Anhang B angegebenen Formen A, B oder C bestimmt.
Die Norm ISO 16269 besteht aus mehreren Teilen, die sich mit verschiedenen Aspekten der statistischen Interpretation von Daten befassen. Zu den weiteren Teilen gehören:
Teil 4: Erkennung und Behandlung von Ausreißern
Teil 7: Median – Schätzung und Konfidenzintervalle
Teil 8: Bestimmung von Prognoseintervallen
Die Norm ISO 16269-6 legt Verfahren zur Ermittlung statistischer Toleranzintervalle fest, die mindestens einen bestimmten Anteil der Grundgesamtheit mit einem bestimmten Konfidenzniveau umfassen.
Es werden sowohl einseitige als auch zweiseitige statistische Toleranzintervalle behandelt, wobei ein einseitiges Intervall entweder eine obere oder eine untere Grenze hat, während ein zweiseitiges Intervall sowohl eine obere als auch eine untere Grenze hat.
Es werden zwei Methoden vorgestellt, eine parametrische Methode für den Fall, dass das untersuchte Merkmal normalverteilt ist, und eine verteilungsfreie Methode für den Fall, dass über die Verteilung nichts bekannt ist, außer dass sie stetig ist.
Außerdem wird ein Verfahren zur Ermittlung zweiseitiger statistischer Toleranzintervalle für mehr als eine Normalverteilungsstichprobe mit gemeinsamer unbekannter Varianz vorgestellt.
Anhang F der Norm enthält Informationen zur Berechnung von Faktoren für zweiseitige parametrische statistische Berechnungen. Zusätzliche technische Informationen finden sich in der Referenz.
Die Bibliographie listet außerdem verschiedene Normen und Veröffentlichungen auf, die für die statistische Interpretation von Daten relevant sind, darunter Normen für die Schätzung des Mittelwerts, Verfahren für die Schätzung und Prüfung in Bezug auf Mittelwerte und Varianzen, die Bestimmung eines statistischen Toleranzintervalls und Tests auf Abweichung von der Normalverteilung.