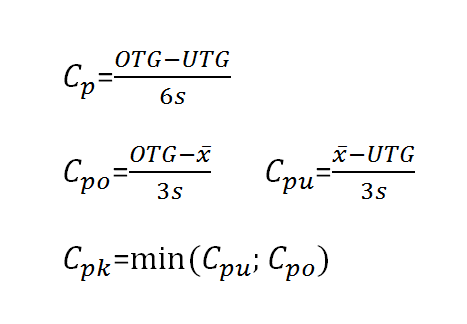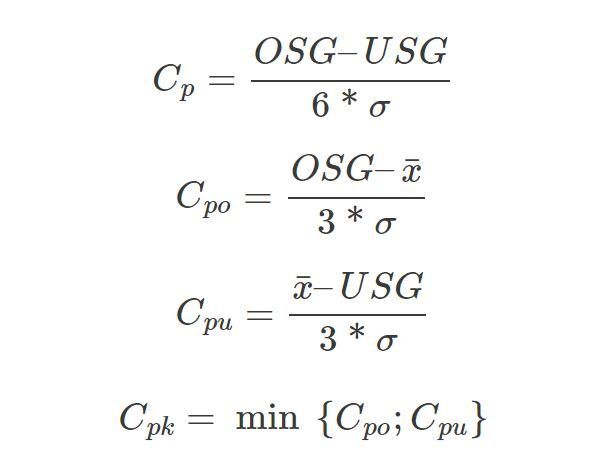Die Prozessfähigkeit cpk, ppk und die Maschinenfähigkeit cmk beschreiben die Fähigkeit ein definiertes Ergebnis zu erzielen.
Sie stehen vor der Aufgabe für Ihren internen oder externen Kunden einen entsprechenden Nachweis erbringen zu müssen?
In diesem Artikel helfen wir Ihnen die Maschinenfähigkeit (cmk) und die Prozessfähigkeit (cpk, ppk) mit validierten Excel Vorlagen zu berechnen.
Wir stellen Ihnen die Werkzeuge zu Verfügung, die:
- in Excel realisiert sind, um Ihnen eine einfache Anpassung und Bedienung der Vorlagen zu ermöglichen
-> Sie sparen Zeit und Geld - Ihnen die Sicherheit bieten, korrekte Ergebnisse auszugeben, weil die Vorlagen mit Minitab und R validiert sind
-> Sie reduzieren Ihr Risiko - praxiserprobt sind und von vielen Unternehmen verwendet werden.
-> Sie reduzieren Ihr Risiko

Die zwei wichtigsten Vorlagen für Ihren Nachweis sind:
Einen Eindruck zur Funktion der Excel Vorlage Maschinenfähigkeit erhalten Sie in diesem Video.
Alternativ als können Sie die Vorlage als Excel add in in englischer oder deutscher Sprache erhalten, falls Sie keine Makros im Unternehmen verwenden dürfen.
Benötigen Sie neben der Berechnung der Normalverteilung auch die Berechnung von einseitigen Toleranzen oder Merkmale mit natürlicher Grenze (Rundheit, Rauheit, etc….) oder benötigen Sie die Vorlage mehrsprachig, ist dies die richtige Vorlage.
Benötigen Sie eine angepasste Vorlage (mit Ihrem Logo, ohne Wasserzeichen, etc.) Schreiben Sie mich hierzu an. Einen schnellen Einblick zu den Berechnungen der „Excel Vorlage kurz“ erhalten Sie in diesem Video.
Werkzeuge zur Prozessfähigkeit und Maschinenfähigkeitsuntersuchung (mfu)
Das gewünschte Ergebnis eines Prozesses wird vom Kunden definiert. Der Kunde erwartet, dass sein Ergebnis dauerhaft erreicht wird. Der Lieferant strebt an, das gewünschte Ergebnis dauerhaft und mit wirtschaftlich vertretbarem Aufwand zu liefern. Dieses Ziel erreicht der Lieferant, indem er seine Prozesse zur Leistungserstellung beherrscht und die entsprechende Prozessfähigkeit herstellt und überwacht. Ein Prozess ist beherrscht, wenn das Ergebnis des Prozesses vorhersagbar ist. Nur ein beherrschter Prozess lässt Aussagen über die Fähigkeit des Prozesses zu.
Die Prozessfähigkeit bezieht sich auf die Fähigkeit eines Produktionsprozesses, reproduzierbare und zufriedenstellende Ergebnisse zu liefern. Ein Prozess kann als fähig angesehen werden, wenn er in der Lage ist, Ergebnisse von gleichbleibend hoher Qualität bei minimaler Varianz und Fehlerrate zu liefern. Ein wichtiger Aspekt der Prozessfähigkeit ist die Fähigkeit, den Prozess kontinuierlich zu verbessern und Anpassungen vorzunehmen, um sicherzustellen, dass er die Anforderungen der Organisation und der Kunden erfüllt.
Der Kunde definiert das gewünschte Ergebnis durch einen zu erreichenden Wert und zwei Spezifikationsgrenzen. Die Grenzen werden als USG (Untere Spezifikationsgrenze) und OSG (Obere Spezifikationsgrenze) bezeichnet. Die Grenzen sind auch als Toleranzgrenzen oder UTG und OTG bekannt.
Die Toleranz, auch Toleranzbreite genannt, stellt den Abstand zwischen USG und OSG dar. Zur Bewertung der Prozessfähigkeit cpk (process capability index) werden die Anforderungen des Kunden mit den Ergebnissen des Prozesses verglichen. Hierbei berechnet man unter der Verwendung eines Modelles der Wahrscheinlichkeit der Normalverteilung den Überschreitungsanteil. Der Überschreitunganteil ist die voraussichtliche Anzahl der Teile pro Million, die ausserhalb der Grenzen der Spezifikation liegen.
Ziel der Berechnung der Prozessfähigkeit ist:
- eine Abschätzung über den Anteil der Daten zu erhalten, die ausserhalb der Toleranzgrenzen sind
- eine Charakterisierung der Fähigkeit eines Prozesses zu erhalten
- eine Abschätzung über die Möglichkeiten zur Prozessverbesserung zu erhalten
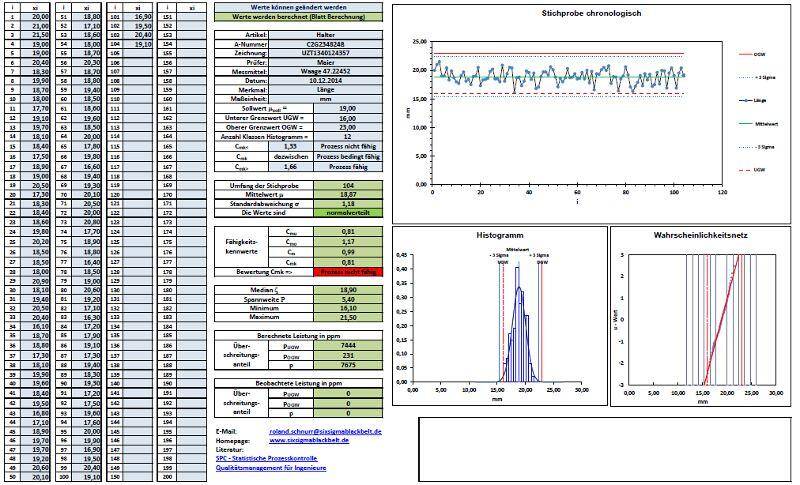
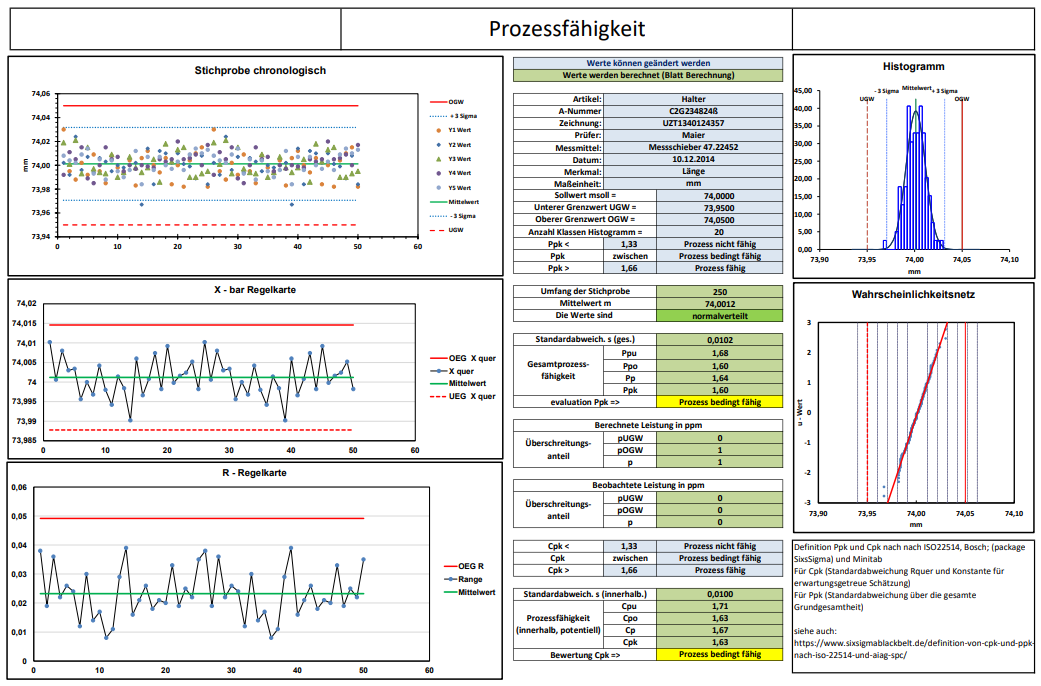
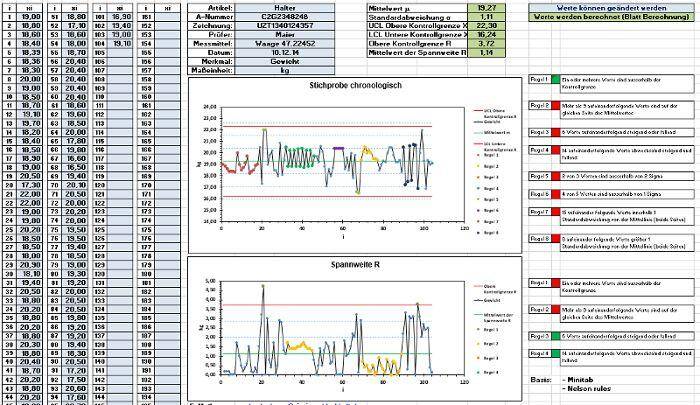
Zur Berechnung der Prozessfähigkeit werden Messdaten benötigt. Die Messdaten zum Vergleich von Anforderung und realem Prozess werden innerhalb des Prozesses erfasst. Zur Auswertung können die Daten in eine Excel Vorlage eingegeben werden. Die Vorlage erstellt automatisch alle Diagramme und berechnet alle Kennzahlen für die Beurteilung der Qualität. Die Normalverteilung der Messwerte ist die Basis für die Berechnung der Daten. Die Aussage ob die Daten normalverteilt sind, erhalten Sie ebenfalls in der Excel Datei.
Benötigen Sie den Nachweis der Maschinen- oder Prozessfähigkeit durch eine Standardsoftware (z. Bsp. Minitab), schreiben Sie eine Mail an mich. Ich helfe Ihnen gerne weiter.
| Version 1 | Version 2 | |
| Ziel | kurzfristige Prozessfähigkeit (Maschinenfähigkeit) | mittel- und langfristige Prozessfähigkeit |
| Anzahl Werte | bis 200 | bis 250 |
| Eingabe Werte | fortlaufend; max 1 Wert pro Probe | bis zu 50 Stichproben mit 2 bis 5 Werten pro Stichprobe |
| Eingabe und Darstellung | 1 Tabellenblatt | 1 Blatt Eingabe 1 Blatt Auswertung |
Excel Vorlage Version 1
Excel Vorlage Version 2
Fähiges Messsystem als Basis für die Prozessfähigkeitsuntersuchung und die Maschinenfähigkeitsuntersuchung (mfu)
Wie bei allen anderen Messungen ist die Basis für Aussagen über den Prozess, die Erhebung zuverlässiger Messdaten. Dazu ist es notwendig, das Messsystem und seine Eignung für die Messaufgabe zu qualifizieren. Dies wird durch eine MSA (Mess – System – Analyse) erreicht. Detaillierte Inhalte zur Messsystemanalyse und Messmittelfähigkeit finden Sie im Beitrag MSA, Messsystemanalyse und Messmittelfähigkeit. Der Beitrag enthält auch die entsprechenden Excel Vorlagen für MSA Verfahren 1 und MSA Verfahren 2.
Aussagen zur Prozessfähigkeit und Maschinenfähigkeit können getroffen werden, wenn folgende Bedingungen erfüllt werden:
Voraussetzungen für die Prozessfähigkeit
1. Es müssen variable Daten vorhanden sein (Gewicht, Breite, Länge, etc.)
2. Es müssen genügend viele Messwerte vorhanden sein
3. Die verwendeten Daten müssen aus einem stabilen Prozess stammen (Test auf Stabilität)
4. Die Daten müssen annähernd der Normalverteilung folgen. (Test auf Normalverteilung)
1. Variable Daten
Datentypen lassen können in variable Daten und attributive Daten unterschieden werden. Variable Daten sind Daten, die gemessen werden können. Dies sind zum Beispiel Gewicht, Breite, Länge, Dicke etc. Attributive Daten sind Daten die sich nicht gemessen werden können, wie z. B. gut oder schlecht. Für diese Daten kann keine Normalverteilung ermittelt werden. Statistische Kennzahlen können hier zu Beispiel Anteile sein (Anteil Gutteile für die Gesamtanzahl der Teile).
2. Genügend viele Messwerte
Die absolute Untergrenze für die Untersuchung eines Wertes zur Prozessfähigkeit liegt bei 50 Werten. Die Ergebnisse der Aussagefähigkeit bei 50 Werten sind jedoch mit einer gewissen Unschärfe behaftet. 50 Werte ist die Anzahl von Messwerten für die Kurzzeitfähigkeitsuntersuchung oder auch Maschinenfähigkeitsuntersuchung.
Für die vorläufige Prozessfähigkeitsuntersuchung beträgt der Mindestumfang 100 Teile. Für die langfristige Untersuchung auf Prozessfähigkeit sind die Empfehlungen in der Übersicht „Prozessfähigkeit nach zeitlichem Ablauf“ dargestellt.
Die Definition der genügenden Anzahl von Messwerten erfolgt in Anlehnung an VDA Band 4 Teil 1[2] und DGQ.
3. Prozessstabilität
Ein Prozess kann durch gewöhnliche und außergewöhnliche Ursachen beeinflusst werden. Gewöhnliche Ursachen ergeben sich aus der natürlichen Prozessstreuung, die in jedem Prozess vorhanden ist. Außergewöhnliche Ursachen sind Ursachen, die nicht als normaler Bestandteil des Prozesses angesehen werden. Sie entstehen durch einmalige oder wiederkehrende Handlungen und Ereignisse. Beispiele sind Änderungen bei der Einstellung von Maschinen, systematische Änderungen in den Rohstoffen, usw.
Der erste Schritt besteht darin, diese außergewöhnlichen Ereignisse im Prozess zu entdecken, zu eliminieren oder unter Kontrolle zu halten. Grundlage für die Trennung von gewöhnlichen von außergewöhnlichen Ursachen ist ein Prozessverständnis für den zu untersuchenden Prozess. Solange die systematischen Ursachen nicht beherrscht sind, ist eine Prozessfähigkeitsuntersuchung nicht sinnvoll. Sind die systematischen Ursachen unter Kontrolle, reduziert sich die Streuung im Prozess auf die gewöhnlichen Ursachen.
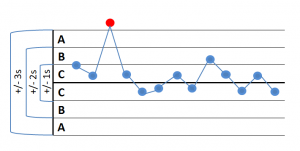
Ein Prozess ist stabil, wenn er keine Streuung durch außergewöhnliche Ursachen auftritt. In der Prozessbeobachtung werden Verlaufsdiagramme oder Regelkarten verwendet, um die Prozessstabilität darzustellen oder außergewöhnliche Werte zu dokumentieren. Die Verlaufsdiagramme oder Regelkarten werden in der Regel auf die 4 wichtigsten Ausnahmebedingungen untersucht:
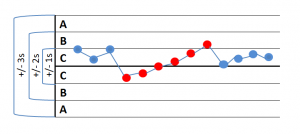
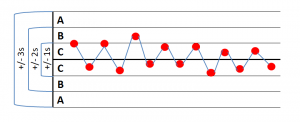
- 1 Punkt mehr als 3S von der Mittellinie entfernt -> Anzeichen für eine Verschiebung des Mittelwertes, der Standardabweichung oder eines einzelnen Ausreissers beim Messen
- 9 aufeinander folgende Punkte auf einer Seite der Mittellinie -> Anzeichen für eine Verschiebung des Mittelwertes
- 6 aufeinander folgende Punkte alle zu oder abnehmend -> Anzeichen für einen Trend
- 14 aufeinander folgende Punkte, abwechselnd auf- und abwärts -> Anzeichen dafür, dass die Daten aus zwei unterschiedlichen Quellen kommen
Wird keine dieser Ausnahmebedingungen erfüllt, gilt der Prozess als stabil. Die erste Bedingung für die Berechnung der Prozessfähigkeit ist erfüllt.
Ich habe eine Excel Vorlage erstellt, die die 8 Regeln der Stabilität testet. Diese Informationen finden Sie im Beitrag Statistische Prozessstabilität.
4. Normalverteilung
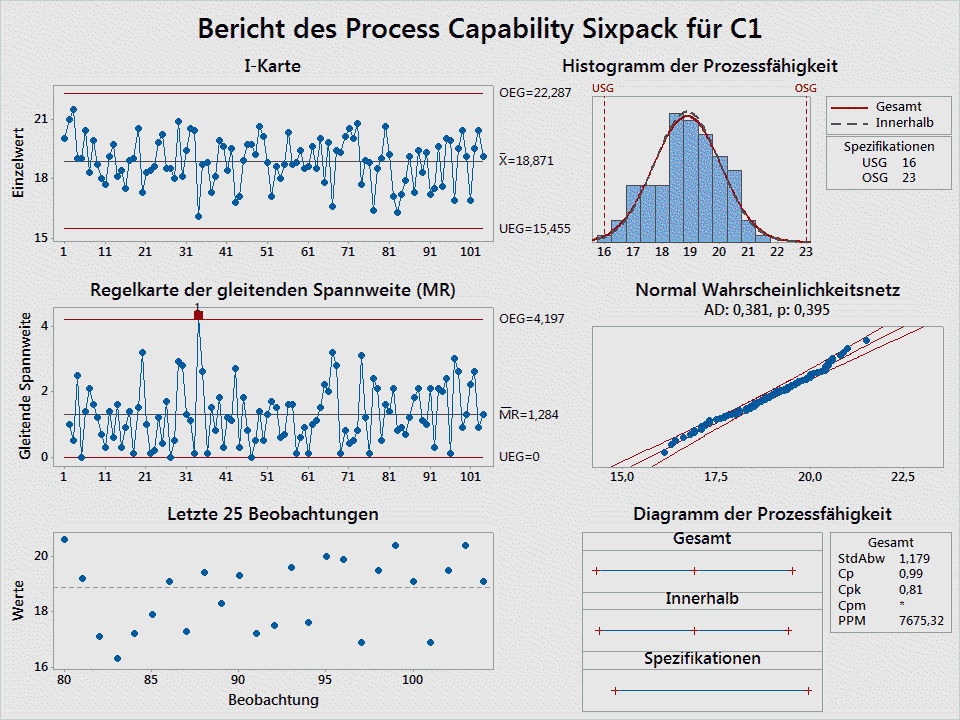
Die Verteilung der Messwerte lassen sich im Histogramm darstellen. Im Histogramm werden die Daten mit Daten zur Normalverteilung ergänzt, sodass sich beide Darstellungen vergleichen lassen. Dies ist eine grobe Betrachtung. Eine genauere Aussage zu Normalverteilung lässt sich durch entsprechende Berechnungen treffen. Eine zusätzliche grafische Möglichkeit zur Darstellung der Normalverteilung bietet das Wahrscheinlichkeitsnetz. Die Diagrammdaten werden in ein Wahrscheinlichkeitsnetz transformiert. Durch die Transformierung der Daten wird ein Diagramm erzeugt. Liegen die Diagrammdaten nahe an der idealisierten Gerade ist von einer Normalverteilung auszugehen.
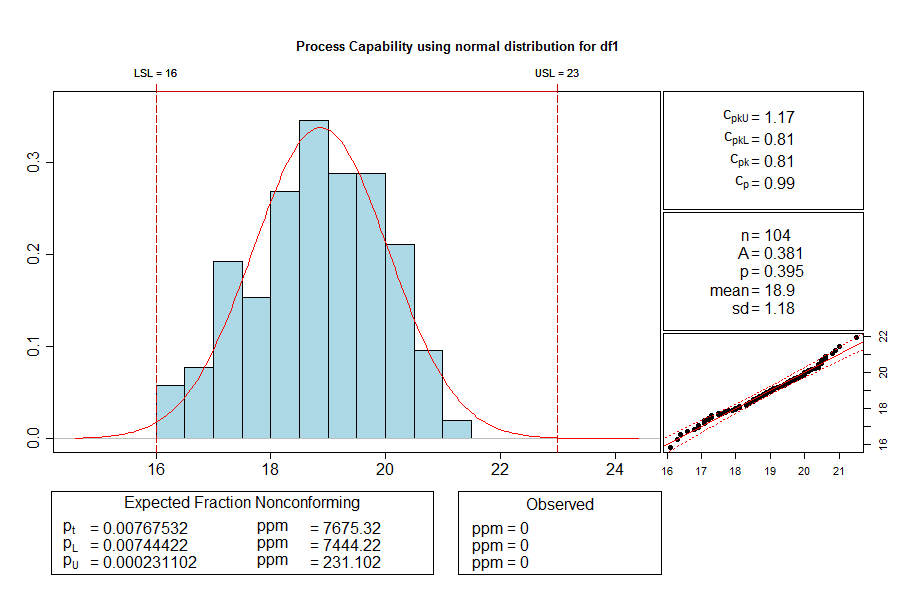
Histogramm und Wahrscheinlichkeitsnetz finden Sie in der Excel Vorlage. Mit der Überprüfung der Daten auf Normalverteilung ist neben der bestätigten Prozessstabilität die zweite Voraussetzung erfüllt, um die Prozessfähigkeit zu berechnen. Die grafische Betrachtung der Normalverteilung übernimmt für Sie die Excel Vorlage. Zur Excel Vorlage zum rechnerischen Test auf Normalverteilung finden Sie im Beitrag „Test auf Normalveteilung Anderson Darling“. Die Tests auf Normalverteilung haben unterschiedliche Eigenschaften hinsichtlich der Art der Abweichungen von der Normalverteilung, die sie erkennen. Als zuverlässiger Test auf Normalverteilung hat sich der Anderson Darling Test bewährt. Der rechnerische Test auf Normalverteilung nehme ich deshalb mit dem Anderson Darling Test vor. Der Test wird auch in der Vorlage zur Maschinen- und Prozessfähigkeit verwendet.
Fähigkeitskennzahlen für nicht normalverteilte Merkmale (Ebenheit, Rundheit, etc.)
Es kann vorkommen, dass Merkmale nicht – normalverteilt sind. Dies gilt insbesondere für die Merkmale:
- Ebenheit
- Rundheit
- Parallelität
- Rechtwinkligkeit
- etc.
Diese Merkmale sind dadurch gekennzeichnet, dass die Merkmale durch einen 0 Wert begrenzt sind. Die Verteilung erfolgt zumeist einer Betragsverteilung 1. Art. Die Prozessfähigkeit wird ausschließlich über den cpk Wert abgebildet.
Möchten Sie die Beitragsverteilung 1. Art wie in den anderen Excel Vorlagen berechnen benutzen Sie die folgende Datei.
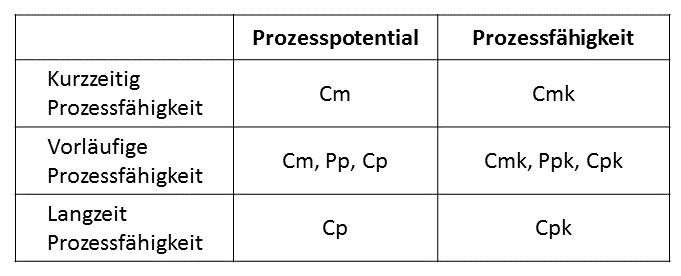
Prozesskennzahlen geordnet nach Prozessphase
Die Fähigkeit und Beherrschbarkeit eines Prozesses wird anhand von Qualitätskennzahlen bestimmt, welche sich aus Mittelwert, Toleranzgrenzen und Streuung ergeben.
Die Unterteilung und Definition der einzelnen Kennzahlen basiert auf den Richtlinien des VDA (Verband der Automobilindustrie e.V.) und der DGQ (Deutsche Gesellschaft für Qualität).
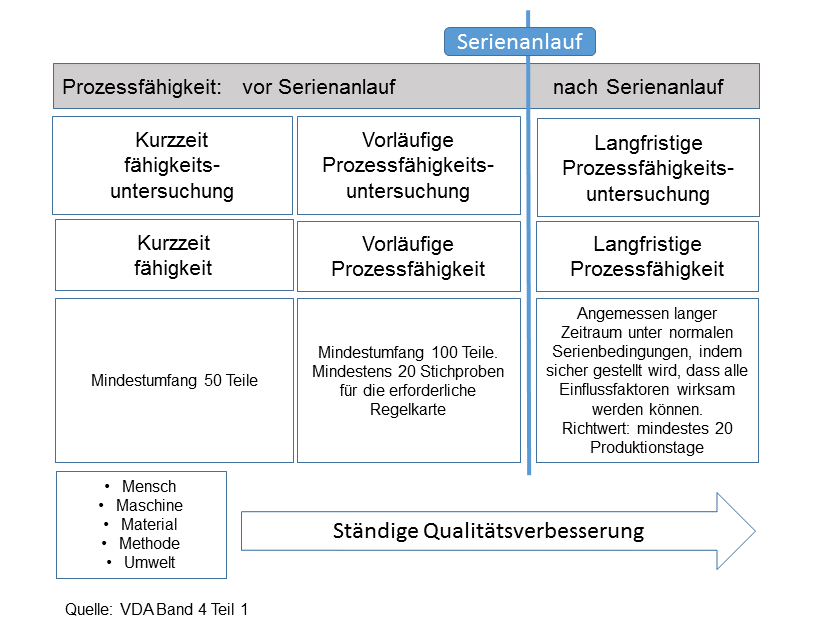
Betrachtet man den zeitlichen Verlauf von Prozessfähigkeit wird allgemein in 2 Gruppen unterteilt:
- Prozessfähigkeit vor Serienanlauf unterteilt in
- Kurzzeitfähigkeit eines Prozesses oder Maschinenfähigkeit
- Vorläufige Prozessfähigkeit
- Prozessfähigkeit nach Serienanlauf gleichbedeutend mit der Langzeit – Prozessfähigkeit
Die Einordnung der einzelnen Untersuchung in den zeitlichen Ablauf stellt folgendes Bild dar.
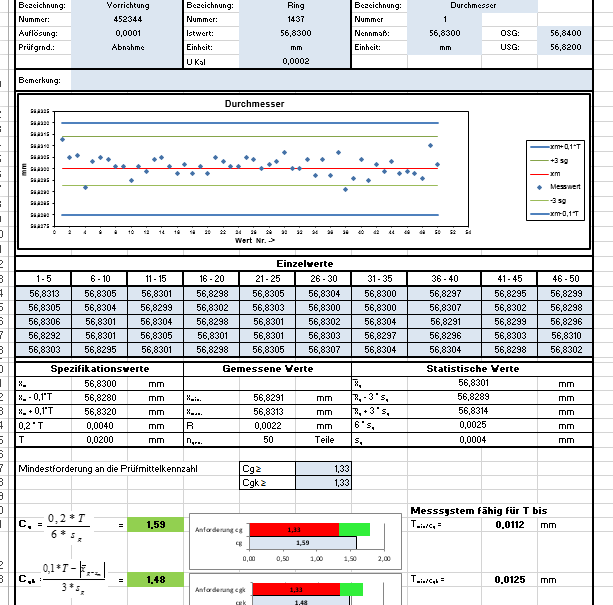
Maschinenfähigkeit mfu oder Kurzzeitfähigkeit eines Prozesses
In der Praxis kann es häufig vorkommen, daß nicht genügend Teile für die Ermittlung der vorläufigen Prozessfähigkeit zu Verfügung stehen. Ist dies der Fall, so wird eine Analyse der Maschinenfähigkeit oder Kurzzeitfähigkeit des Prozesses, durchgeführt. Häufig ist dies der Fall bei Vorabnahmen von Fertigungseinrichtungen beim Hersteller oder beim Einfahren von Fertigungsprozessen.
Bei der Maschinenfähigkeitsuntersuchung mfu werden alle Parameter (Mensch, Methode, Material und Mitwelt) konstant gehalten, sodass möglichst nur der Einfluss der Maschine auf das Ergebnis gemessen werden kann. Dies bedeutet es gibt:
- keine Wechsel der Maschinenbediener
- keine Veränderung in der Bedienung der Maschine
- Keine Änderung der Materialcharge
- möglichst konstante Umgebungsparameter
- etc.
Einflüsse, die sich nicht vermeiden lassen und die nicht zufällig sind, werden dokumentiert. Diese Einflüsse werden anschließend separiert und geordnet.
Ermittelt wird eine vorläufige Aussage über die Eignung des Prozesses. Die Kennzahl für die Maschinenfähigkeit ist der cmk Wert. Der cmk Wert ergibt sich aus dem Minimum von cmu und cmo.
Normalerweise werden hierzu 50 aufeinander folgende Teile aus dem Prozess entnommen. Die zeitliche Abfolge der Teile wird dokumentiert, um eventuelle Trends zu erkennen. Die 50 Teile werden auch zur Prüfung auf die Verteilungsform der Messergebnisse verwendet.
Vorläufige Prozessfähigkeit
Die vorläufige Prozessfähigkeitsuntersuchung dient dazu einen Prozess vor Serienanlauf zu betrachten. Sie hilft gleichzeitig dabei die oberen und unteren Eingriffsgrenzen des Prozesses zu deklarieren. Methodik: Der Prozess wird über einen längeren Zeitraum gefahren. Während der Prozessierung entnimmt man in regelmässigen Abständen Stichproben. Als Richtwert gilt die Entnahme von 25 Stichproben mit jeweils fünf Teilen. Das Minimum beträgt 20 Stichproben mit jeweils drei Teilen.
Mithilfe einer Qualitätsregelkarte wird beurteilt, ob der Prozess beherrscht ist. Gleichzeitig können über zusätzliche Analysen die Messwerte ausgewertet werden. Hilfreich sind hierbei:
Bereits in dieser Phase der Analyse sollte der Prozess unter den zukünftigen Serienbedingungen produzieren. Alle Einflüsse der Serie sollten möglichst schon vorhanden und wirksam sein. Gleichzeitig sollten die Methoden und Formeln zur Berechnung der einzelnen Fähigkeitszahlen bereits bei Ermittlung der kurzzeitigen Fähigkeit und bei der Berechnung der Maschinenfähigkeit verwendet werden. Nur so ist eine sinnvolle Verbindung der einzelnen Analysen im zeitlichen Ablauf sichergestellt. [4]
Langzeit Prozessfähigkeit
Die Langzeit – Prozessfähigkeitsindex cpk definiert die Ergebnisse des Prozesses nach dem Anlauf der Serie. Methodik: Die Langzeit-Prozessfähigkeitsuntersuchung soll die die Qualitätsfähigkeit unter realen Bedingungen beurteilen. Sie erstreckt sich deshalb über einen längeren Zeitraum. Im Idealfall werden Stichproben verteilt über 20 Tage der Produktion entnommen. Die Verfahrensweise entspricht der Analyse zur kurzfristigen Prozessfähigkeit.
Die Excel Vorlage
(Excel mit Makros) ist hierzu das ideale Hilfsmittel.
Kurzfristige und langfristige Prozessfähigkeitsuntersuchungen analysieren den Herstellungsprozess hinsichtlich der Eignung, die geplante Fertigungsaufgabe innerhalb der vorgegebenen Qualitätsanforderungen zu erfüllen. Hierbei treten in der langfristigen Prozessfähigkeitsuntersuchung auch die einzelnen Einflüsse der 5 Einflussarten wesentlich stärker zutage als in der Kurzfristuntersuchung.
Berechnung der Qualitätskennzahlen
Die Qualitätsfähigkeitskennzahlen werden wie folgt unterschieden.
Die Formel für die Berechnung der einzelnen Kennzahlen ändert sich nicht im Bezug auf die Zeit. Unabhängig von der Zeit sind die Formeln für Cm = Pp = Cp. Es ändert sich lediglich der Umfang der Messwerte. Die gleiche Vorgehensweise gilt für die Formeln für Cmk = Ppk = Cpk.
Beispielhaft erkläre ich die Berechnung der Kennzahlen anhand der Langzeit Prozessfähigkeit.
Die Langzeit Prozessfähigkeit wird durch den cp Wert (process capability) und den cpk Wert (critical process capability) beschrieben. Die Kenngrössen werden nach folgenden Formeln ermittelt.
CP = Prozessstreuung
CPO = Prozesstreuung obere Toleranzgrenze
CPU = Prozesstreuung untere Toleranzgrenze
CPK = Prozessstreuung und Lage
OTG = Obere Toleranzgrenze
UTG = untere Toleranzgrenze
x quer = Mittelwert
s = Standardabweichung
CP Wert
Der Cp Wert beschreibt das Prozesspotential. Die Kennzahl cp ist ein Mass für die Breite der Prozessstreuung im Verhältnis zur Toleranzbreite. Die Toleranzbreite ist der Bereich zwischen dem oberen und unteren Grenzwert. Als Breite der Prozessstreuung wird in der Regel die dreifache Standardabweichung nach oben oder unten um den Mittelwert verwendet. Innerhalb dieses Bereiches werden bei einem beherrschten Prozess mehr als 99% aller Werte erwartet.
Der cp Wert liegt bei 1, wenn der Prozessstreubereich der Toleranzgrenze (Oberer-/ Unterer Grenzwert) entspricht. Die Berechnung des cp Wert ist nicht ausreichend für die Beurteilung der Qualitätsfähigkeit eines Prozesses, da er nicht die Lage des Prozesses berücksichtigt. Hierzu wird der cpk Wert verwendet.
Prozessfähigkeitsindex CPK Wert
Der cpk Wert (process capability value) ist gleich der Prozesspotentials cp, berücksichtigt jedoch zusätzlich die Lage der Verteilung. Hierzu wird der kritische Abstand zwischen Prozesslage und Toleranzgrenze berechnet. Der Prozessfähigkeitsindex cpk Wert ist so definiert, dass er gleich dem cp Wert ist, wenn der Prozess in der Toleranzmitte zentriert ist. Der cpk Wert entspricht dem kleineren oder kritischeren Werte von cpo oder cpu. Ist der cpk Wert kleiner als der cp Wert bedeutet dies, dass der Mittelwert der Verteilung ausserhalb der Toleranzmitte liegt. Ist cp grösser als der Prozessfähigkeitsindex cpk , so kann der Prozess durch eine Zentrierung fähig gemacht werden. Die Prozessfähigkeit bewertet somit cp und cpk, um eine valide Aussage zu machen.
Möchten Sie wissen, welche Werte Mittelwert und Standardabweichung erfüllen müssen um einen Zielwert cp oder einen Zielwert cpk zu erreichen, können Sie die Excel Vorlage aus dem Beitrag „cp und cpk berechnen“ verwenden.
Eine Untersuchung der Fähigkeit darf nur bei beherrschten Prozessen erfolgen. Der Prozessfähigkeitsindex cpk ist ein Mass für die Merkmalslage und Streuung der Merkmale. Die Lage und Streuung beinhaltet Einflussfaktoren die durch die 5 M, Mensch, Maschine, Methode, Material und Mitwelt ausgelöst werden. Der cpk Wert ist somit eine gute Messgrösse, um die Auswirkungen von verschiedenen Einflussfaktoren zu analysieren, ist das Ishikawa oder Ursache – Wirkungs – Diagramm.
Zusammenhang Cpk und Ausschuss in % und ppm
Die Fähigkeitsindizes cp und cpk dienen der Prozesslenkung. Sie ermöglichen eine statistische Prozesslenkung durch die Kombination von Mittelwert und Standardabweichung. Man vergleicht die Fähigkeitsindizes mit den Forderungen des Kunden und ermöglicht dadurch eine Voraussage zur Fähigkeit des Prozesses.
Kann die Fähigkeit eines Prozesses nicht nachgewiesen werden, so sind keine Aussagen über die Fehlerfreiheit des Outputs möglich. Sind keine Aussagen über die Fehlerfreiheit im Vorfeld möglich und sollen nur gute Output – Ergebnisse weitergereicht werden, so ist eine 100% Kontrolle der Ergebnisse unumgänglich.
Ist eine Kontrolle des Ergebnisse nur über eine zerstörerische Prüfung möglich, so müsste der komplette Output, da 100 % Kontrolle zerstörerisch geprüft werden und wäre somit zerstört. Basis für Stichprobenprüfung ist häufig die Maschinen- oder Prozessfähigkeit.
Kann ein cpk berechnet werden, so können Voraussagen zum Ausschuß des Prozesses gemacht werden. Eine Normalverteilung vorausgesetzt, ergeben sich für die cpk Werte entsprechende Ausschussmengen. Der cpk 1,67 ist ein Wert der eine sehr geringe Ausschussmenge von 0,57 ppm (parts per million) ergibt. Ein cpk 1,33 ergibt einen ppm von 63. Die folgende Tabelle zeigt den Ausschuss in Prozent oder in absoluten Zahlen für bestimmte cpk Werte.
| Anzahl Sigma bis zu den Toleranzgrenzen | cpk – Wert | Ausschuss in % | Ausschuss in ppm |
| 1 | 0,33 | 32 % | 320000 |
| 2 | 0,67 | 4,60 % | 46000 |
| 3 | 1,00 | 0,27 % | 2700 |
| 4 | 1,33 | 0,0063 % | 63 |
| 5 | 1,67 | 0,000057 % | 0,57 |
| 6 | 2,00 | 0,0000002 % | 0,002 |
Prozessfähigkeit bei einseitiger Toleranz
Hat ein Merkmal auf einer Seite eine Spezifikationsgrenze kann keine Toleranzbreite angegeben werden. Deshalb kann bei einseitiger Toleranz immer nur der Cpk-Wert (process capability value) berechnet werden.
Ist eine obere Spezifikationsgrenze angegeben entspricht der Prozessfähigkeitsindex Cpk = Cpko. Ist eine untere Spezifikationsgrenze angegeben entspricht der Cpk = Cpku.
Im Anhang finden sich noch Informationen zu dem Verhalten der Prozessfähigkeit bei technisch begrenzten Merkmalen [3].
Eine Vorlage zur Berechnung der Prozessfähigkeit bei einseitiger Toleranz können Sie hier herunterladen.
Prozessfähigkeit und Maschinenfähigkeit mit Minitab Software
Minitab ist das Standardpaket im Bereich Statistik.
Prozessfähigkeit und Maschinenfähigkeit mit der Statistik Software R
Test auf Normalverteilung, sowie Histogramm und statistische Werte
Sollten Sie keine Möglichkeiten haben Excel zu verwenden, so empfiehlt sich als Alternative die frei verfügbare Statistik Software R.
Für die Daten der Excel Vorlage von weiter oben, benutze ich nun R als Statistik Software für die Auswertungen.
Nachdem Sie R installiert haben, installieren Sie das Erweiterungs Packet qualitytools. Nach entsprechender Vorbereitung der Daten erhalten Sie durch die Ausführung des Befehls cp folgende Auswertung.
# Daten aus der Excel Datei maschinen.xlsx in die Tabelle df1 einlesen
# Anschließend die cp Funktion aus der library qualitytools aufrufen
library(openxlsx)
library(qualityTools)
xlsxFile <- („C://Users//ThinkPad User//Daten//R Statistik//maschinen.xlsx“)
df1 <- read.xlsx(xlsxFile = xlsxFile, sheet = 1, startRow = 1, skipEmptyRows = FALSE)
cp(df1$mm,,23,16)
Zeitreihen plotten mit der Statistik Software R
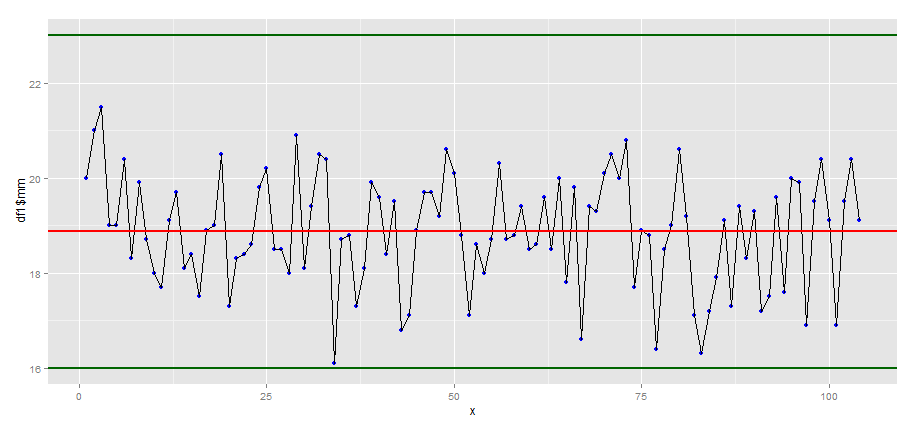
Das Paket ggplot2 muß installiert und aktiviert sein. Dann beginnen wir mit der Erstellung des Diagrammes zur Zeitreihe.
# Daten sind bereits in der Tabelle df1
# definieren des Datenbereiches
# Packet ggplot2 wird initialisiert
library(ggplot2)
# Berechnen der Anzahl der Werte im Wertebereich
AnzahlWert <- length(df1$mm)
x<-(1:AnzahlWert)
# definieren des Datenbereiches
g<-ggplot(df1, aes(x,df1$mm))
# definieren der Datenpunkte
g<- g + geom_point()
g<- g + geom_point(colour=“blue“, size= 2)
# definieren der Verbindungslinie zwischen den Datenpunkten
g<- g + geom_line(colour= „black“)
# definieren des oberen Grenzwertes als Linie
g<- g + geom_hline(yintercept=23 ,colour= „darkgreen“, size = 1 )
# definieren des unteren Grenzwertes als Linie
g<- g + geom_hline(yintercept=16 ,colour= „darkgreen“, size = 1 )
# berechnen des Mittelwertes und Eintragen in das Diagramm
Mittelwert <- mean(df1$mm)
g<- g + geom_hline(yintercept= Mittelwert ,colour= „red“, size = 1 )
Sie erhalten damit folgende Grafik
Mittlerweile benutze ich die Statistik Software R oft, um die Ergebnisse aus Excel zu vergleichen. Ich finde R ganz nützlich, obwohl es einige Zeit für die Einarbeitung benötigt.
Zusammenfassung Formeln
Für alle nachfolgenden Formeln gilt:
Zuerst ist die Frage zu klären, welche Verteilung vorliegt.
Normalverteilung
Die Daten entsprechen einer Normalverteilung, und es ist sowohl USG wie OSG für den Prozess relevant. Es gilt:
Die Daten entsprechen einer Normalverteilung und USG ist nicht relevant, da eventuell eine technische Grenze vorliegt, zum Beispiel USG = 0 weil die Toleranz eine Ebenheit darstellt und die Messwerte nicht kleiner 0 werden können.
Es gilt:
Cpk = Cpo
Die Daten entsprechen einer Normalverteilung und OSG ist nicht relevant, da keine OSG vorliegt.
Es gilt
Cpk = Cpu
Betragsverteilung 1. Art
Die Daten entsprechen einer Betragsverteilung 1. Art[1], zum Beispiel 0 begrenztes Merkmal Ebenheit, so gilt hier die Betragsverteilung 1. Art zu berechnen. Als Basis für den Cpk wird die berechnete Verteilung herangezogen. Anschließend wird das 50 % Quantil und das 99,865 % Quantil der Verteilung bestimmt. Die Berechnung des Cpk erfolgt dann über folgende Formel:
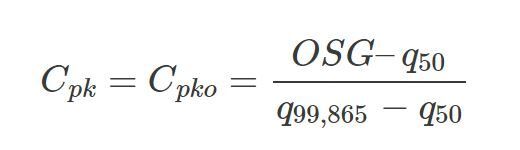
Die Werkzeuge zur Messsystemanalyse -> Maschinenfähigkeit -> Prozessfähigkeit
- Messsystemanalyse
- Maschinenfähigkeit und Prozessfähigkeit
- Statistische Prozesskontrolle SPC
- Regelkarte
Quellen / Referenzen:
Die AIAG ist ein Anbieter für weiterführende Kurse im Bereich SPC.
Dietrich, E., & Schulze, A. (2009). Statistische Verfahren zur Maschinen- und Prozessqualifikation: Mit 61 Tabellen (6., vollst. überarb. Aufl). Hanser. ISBN 978-3-446-41525-6
[1] Design for Six Sigma: Betragsverteilung 1. Art. (o. J.). Abgerufen 15. April 2022, von https://www.eit.hs-karlsruhe.de/dfss/statistics/univariate-wahrscheinlichkeitstheorie/spezielle-stetige-verteilungen/betragsverteilung-1-art.html
[2] Band 04 Abschnitt 1, Allgemeines 08/2020. (o. J.). VDA QMC Webshop. Abgerufen 12. April 2022, von https://webshop.vda.de/QMC/band-04-abschnitt-1-allgemeines-082020
[3] Bredner, B. (o. J.). Prozessfähigkeit bei technisch begrenzten Merkmalen. 15.
[4] Pearn, W. L., & Kotz, S. (2006). Encyclopedia and handbook of process capability indices: A comprehensive exposition of quality control measures. World Scientific.
Weitere wichtige Inhalte für Ihr Projekt!
Folgen Sie den einzelnen, unten stehenden Links und Sie gelangen zum Thema und den entsprechenden Excel Dateien. Das Bild mit allen Links zu den Themen können Sie als pdf (Werkzeuge_20150722_4_als_pdf) downloaden.
Die Excel Vorlagen für die Lean Tools laden Sie in dieser Excel Datei (Toolbox.xlsx) runter.
Das Komplettpaket Excel Vorlagen Messsystemanalyse und Prozessfähigkeit können Sie hier anfordern.
Organisieren – Define Phase
- Projektauftrag
- Wasserfall Diagramm
- Stichprobe berechnen
- Business Case
- Pareto Prinzipg 80/20 Regel
- Z Wert Tabelle
- Change Management
Messen – Measure Phase
- Pareto Diagramm
- Konfidenzintervall
- Six Sigma Organisation
- Boxplot Diagramm
- Ursache Wirkungs Diagramm
- Smart Regel
- Qualitäts Kennzahlen
- Ishikawa Diagramm
- Projektabgrenzung
- Prozesskennzahlen
- Zeitanalyse
- Kick off
- OEE Gesamtanlagen- effektivität
- Sipoc
Analysieren – Measure Phase
- Messsystemanalyse Verfahren 1
- Messsystemanalyse Verfahren 2
- Messsystem fähig?
- Messsystem Analyse Verfahren 3
- Projektplan
- Messwert normalverteilt Anderson Darling
- Wahrscheinlichkeitsnetz
- Prozess / Maschine fähig? cp / cpk ausreichend?
- SPC Statistische Prozesskontrolle
Verbessern – Improve Phase
- 7 Arten der Verschwendung
- Paarweiser Vergleich Nutzwert Analyse
- Spaghetti Diagramm
- 5S Methode
- EPEI Every part every interval
- Wertstromanalyse Symbole
- Little’s Law
- Yamazumi chart Yamazumi board
- Wertstromanalyse
- 10er Regel der Fehlerkosten