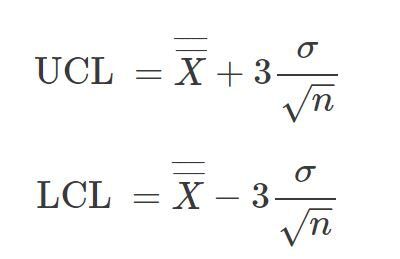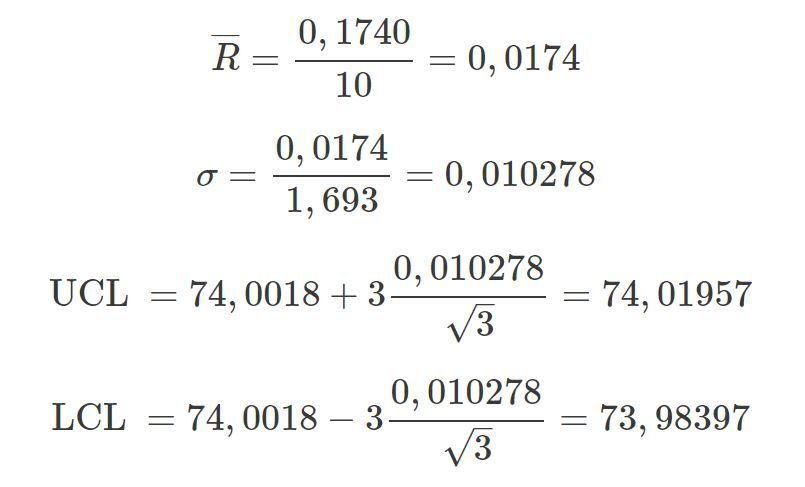Regelkarte Prozessregelkarte Qualitätsregelkarte

Eine Qualitätsregelkarte (QRK) ist ein grafisches Hilfsmittel zur Überwachung von Fertigungsprozessen auf statistischer Basis. Die Qualitätsregelkarte wird verwendet, um einen Prozess über einen Zeitraum hinweg fortlaufend zu beobachten und zu bewerten.

Die Regelkarte stellt statistische Werte zur Bewertung von Prozessen dar und dient der Prozessregelung. Dazu werden statistische Stichprobenkennwerte (z. B. Stichprobenmittelwert und Stichprobenstandardabweichung des Qualitätsmerkmals) und Warn-, Eingriffs- und Toleranzgrenzen grafisch dargestellt.

Was sind die Vorteile der Qualitätsregelkarte?

Die Qualitätsregelkarte bietet eine einfache grafische Möglichkeit zur Beobachtung der Prozessleistung. Durch den Vergleich der einzelnen Messwerte mit den berechneten Kontrollgrenzen und Eingriffsgrenzen kann festgestellt werden, ob der Prozess statistisch beherrscht und unter Kontrolle ist.

Die Regelkarte ist ein wesentliches Werkzeuge für die Statistische Prozesslenkung (SPC – englisch statistical process control) zur Optimierung von Produktions- und Serviceprozessen.

Sie erleichtert die Beobachtung und Erkennung von gewöhnlicher und spezieller Variation. Die Qualitätsregelkarte gibt die Richtung für die Ursachenforschung vor. Je nach Variation in der Regelkarte werden unterschiedliche Ansätze zur Beeinflussung des Prozesses gewählt.

Im Rahmen von Six Sigma Projekten werden Regelkarten häufig in der Kontrollphase des Projektes eingesetzt. Sie ermöglichen durch eine einfache Prozesskontrolle den Nachweis der Nachhaltigkeit der Lösung im Prozess.

Darüber hinaus gibt die Regelkarte Hinweise, in welche Richtung der Prozess verbessert werden muss, um letztendlich ein besseres Endergebnis für den Prozess zu erzielen.

Der Einsatz von Qualitätsregelkarten eignet sich besonders für die Produktion großer Stückzahlen. Der Anwender kann die Prozesskontrolle und -regelung selbst durchführen und muss nicht auf einen externen Experten warten.

[toc]

Auswahl der richtigen Regelkarte

Es gibt verschiedene Arten von Regelkarten. Ein wichtiger Hinweis für die Auswahl der richtigen Regelkarte, ist die Art der verwendeten Daten. Hier wird zwischen stetigen und diskreten Daten unterschieden. Neben der Art der Daten ist die Anzahl der Teile in der Stichprobe ein Kriterium für die Auswahl der richtigen Regelkarte.

Die Auswahl der geeigneten Regelkarte erfolgt anhand der folgenden Tabelle:

Stetige Daten (Temperatur, Kosten, Zeit, Zahlen)	Stichprobengröße =1	I / MR
Kleine Stichprobengröße <10 (in der Regel 3 -5); konstant	X quer / R
Große Stichprobengröße >10 oder variable Stichgröße	X quer / S

Diskrete Daten (Anzahl Fehler, Fehleranteil)	Fehler pro Teil	Konstante Stichprobengröße (Anzahl Fehler >5)	C – Karte
Variable Stichprobengröße	U – Karte
Fehlerhafte Teile	Konstante Stichprobengröße >50	NP – Karte
Variable Stichprobengröße >50	P – Karte

Festlegung der Randbedingungen

Bevor mit der eigentlichen Erstellung der Qualitätsregelkarte begonnen wird, müssen die Häufigkeit und das Verfahren der Probenahme genau festgelegt werden. Alle Stichproben müssen nach dem Zufallsprinzip und unter den gleichen technischen Bedingungen entnommen werden. Die Häufigkeit ist in Abhängigkeit vom Merkmal festzulegen, z. B. stündlich, täglich, pro Schicht.

Für jede Einzelstichprobe werden dann die benötigten statistischen Werte berechnet.

Erstellung der Regelkarte

Tabelle Konstante für Berechnung der Eingriffsgrenzen der Regelkarte

Tabelle der Konstanten für die Berechnung der Eingriffsgrenzen der Regelkarte. Die Konstanten basieren auf einer statistischen Sicherheit von 99,73 %

n	A2	D2	D3	D4	A3	C4	B3	B4
2	1,88	1,128	–	3,267	2,659	0,7979	0	3,267	1,88
3	1,023	1,693	–	2,574	1,954	0,8862	0	2,568	1,187
4	0,729	2,059	–	2,282	1,628	0,9213	0	2,266	0,796
5	0,577	2,326	–	2,114	1,427	0,94	0	2,089	0,691
6	0,483	2,534		2,004	1,287	0,9515	0,03	1,97	0,548
7	0,419	2,704	0,076	1,924	1,182	0,9594	0,118	1,882	0,508
8	0,373	2,847	0,136	1,864	1,099	0,965	0,185	1,815	0,433
9	0,337	2,97	0,184	1,816	1,032	0,9693	0,239	1,761	0,412
10	0,308	3,078	0,223	1,777	0,975	0,9727	0,284	1,716	0,362
11	0,285	3,173	0,256	1,744	0,927	0,9754	0,321	1,679	–
12	0,266	3,258	0,283	1,717	0,886	0,9776	0,354	1,646	–
13	0,249	3,336	0,307	1,693	0,85	0,9794	0,382	1,618	–
14	0,235	3,407	0,328	1,672	0,817	0,981	0,406	1,594	–
15	0,223	3,472	0,347	1,653	0,789	0,9823	0,428	1,572	–
16	0,212	3,532	0,363	1,637	0,763	0,9835	0,448	1552	–
17	0,203	3,588	0,378	1,622	0,739	0,9845	0,466	1,534	–
18	0,194	3,64	0,391	1,608	0,718	0,9854	0,482	1,518	–
19	0,187	3,689	0,403	1,597	0,698	0,9862	0,497	1,503	–
20	0,18	3,735	0,415	1,585	0,68	0,9869	0,51	1,49	–
21	0,173	3,778	0,425	1,575	0,663	0,9876	0,523	1,477	–
22	0,167	3,819	0,434	1,566	0,647	0,9882	0,534	1,466	–
23	0,162	3,858	0,443	1,557	0,633	0,9887	0,545	1,455	–
24	0,157	3,895	0,451	1,548	0,619	0,9892	0,555	1,445	–
25	0,153	3,931	0,459	1,541	0,606	0,9896	0,565	1,435	–

 

Regelkarte für stetige Daten

X quer / R Regelkarte

Anbei finden Sie die X quer / R Regelkarte als Excel Vorlage zum Download. In der Regelkarte finden Sie auch ein Beispiel, zur Berechnung der Eingriffsgrenzen in Excel. Das Beispiel der Eingriffsgrenzen können Sie in der Vorlage an Ihre Bedürfnisse anpassen.

Eine Regelkarte ist ein Diagramm zur grafischen Darstellung statistischer Kenngrößen. Eine Regelkarte enthält eine Mittellinie und Kontrollgrenzen. Die Mittellinie wird durch den Mittelwert bestimmt. Die Kontrollgrenzen werden mit Hilfe der Standardabweichung berechnet.

Die Aufgabe von Regelkarten ist es, den Mittelwert und die Standardabweichung eines Prozesses abzuschätzen. Der Mittelwert ist einfach zu berechnen und zu verstehen. Der Mittelwirt ist einfach der Durchschnitt aller Ergebnisse. Die Standardabweichung ist ein wenig schwieriger zu verstehen. Es gibt verschiedene Möglichkeiten die Standardabweichung zu berechnen.

Je nach Berechnung der Standardabweichung ergeben sich unterschiedliche Kontrollgrenzen.

Untergruppen der Werte

Die Daten, die wir verwenden werden, sind in der Tabelle aufgeführt. Wir haben 10 Untergruppen, die jeweils 3 Beobachtungen oder Ergebnisse enthalten.

Untergruppe	X1	X2	X3	Untergruppe Durchschnitt	Untergruppe R	Untergruppe s
1	74,0300	74,0020	74,0190	74,0170	0,0280
2	73,9950	73,9920	74,0010	73,9960	0,0090
3	73,9880	74,0240	74,0210	74,0110	0,0360
4	74,0020	73,9960	73,9930	73,9970	0,0090
5	73,9920	74,0070	74,0150	74,0047	0,0230
6	74,0090	73,9940	73,9970	74,0000	0,0150
7	73,9950	74,0060	73,9940	73,9983	0,0120
8	73,9850	74,0030	73,9930	73,9937	0,0180
9	74,0080	73,9950	74,0090	74,0040	0,0140
10	73,9980	74,0000	73,9900	73,9960	0,0100
			Summe	740,0177	0,1740
			Durchschnitt	74,0018	0,0174

Die Untergruppengröße ist für jede der 10 Untergruppen konstant. Der Untergruppendurchschnitt, die Spannweite und die Standardabweichung wurden ebenfalls für die unten angegebene Verwendung berechnet. Die Gesamtsumme und der Gesamtmittelwert werden für die Untergruppendurchschnitte, die Untergruppen – Spannweiten und die Untergruppenstandardabweichungen angegeben. Aufgrund von Rundungen können sich geringfügige Abweichungen ergeben.

Möglichkeiten zur Schätzung der Standardabweichung

Im Folgenden werden drei verschiedene Möglichkeiten zur Schätzung der Standardabweichung betrachtet. Diese beeinflussen, wie die Kontrollgrenzen berechnet werden. Die Kontrollgrenzen für die X-Karte sind gegeben durch:

Kontrollgrenzen basierend auf Sigma

wobei UCL und LCL die obere und untere Kontrollgrenze, n die Untergruppengröße und σ die geschätzte Standardabweichung der Einzelwerte ist. Zur Erinnerung: Die Standardabweichung der Untergruppenmittelwerte ist gleich der Standardabweichung der Einzelwerte dividiert durch die Quadratwurzel der Untergruppengröße. Diese Gleichungen zur Berechnung der Kontrollgrenzen können sich von den Gleichungen unterscheiden, die Sie normalerweise verwenden.

Der Wert von σ hängt von der Methode ab, die Sie zu seiner Schätzung verwenden. Wir werden uns drei Methoden zur Schätzung von σ für Untergruppendaten betrachten:

• Mittelwert der Untergruppenbereiche
• Mittelwert der Standardabweichungen der Untergruppe
• Gepoolte Standardabweichung

A. Durchschnitt der Untergruppenbereiche

Der Mittelwert der Untergruppenbereiche ist die klassische Methode zur Schätzung der Standardabweichung. Der Mittelwertbereich ist einfach der Mittelwert der Subgruppen-Mittelwerte, wenn die Subgruppengröße konstant ist:

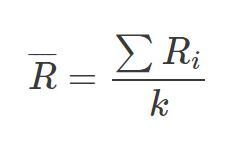
wobei R_i der Bereich der i-ten Untergruppe und k die Anzahl der Untergruppen ist. Die Standardabweichung wird dann mit der folgenden Gleichung geschätzt:

und Sigma

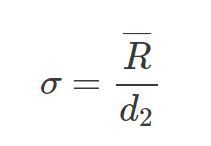
wobei d₂ eine Konstante ist, die von der Größe der Untergruppe abhängt.

Tabelle 2 zeigt die Werte von d₂ basierend auf Subgruppengrößen bis zu 10. Aus der Tabelle können Sie ersehen, dass d₂ für eine Subgruppengröße von 3 1,693 beträgt.

n	d2	c4
2	1,128	0,7979
3	1,693	0,8862
4	2,059	0,9213
5	2,326	0,9400
6	2,534	0,9515
7	2,704	0,9594
8	2,847	0,9650
9	2,970	0,9693
10	3,078	0,9727

Anhand der Schätzung der Standardabweichung vom Mittelwertbereich berechnen wir die Kontrollgrenzen mit folgender Formel:

Für die obere Kontrollgrenze

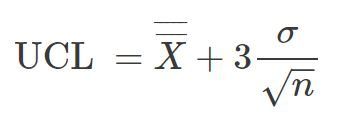
Für die untere Kontrollgrenze

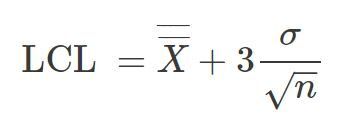
Für obiges Beispiel:

Wollen Sie die Berechnung Excel überlassen erfahren Sie hier mehr zur Regelkarte incl. einer entsprechenden Excel Vorlage.

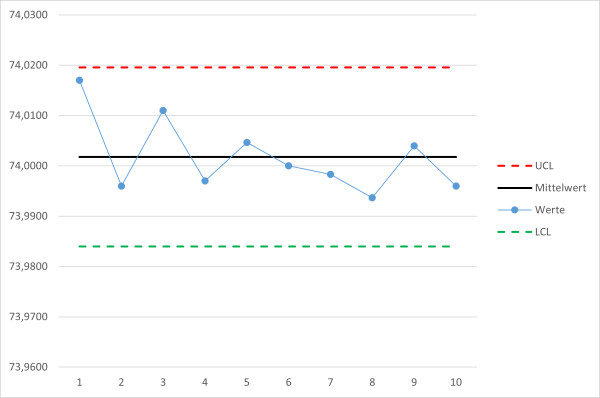
Diagramm X quer Regelkarte

Als Diagramm der Regelkarte erhalten wir folgende Darstellung

 

Auswerten von Regelkarten

Systematische Abweichungen unterliegen Gesetzmäßigkeiten. Aus dem Verlauf der Messpunkte auf der Qualitätsregelkarte kann auf diese Gesetzmäßigkeiten geschlossen werden.

So spricht man von einem „Trend“, wenn mindestens sieben Messpunkte eine annähernd lineare Steigung in Richtung einer Grenze aufweisen. Möglicherweise liegt ein stark ansteigender Werkzeugverschleiß vor, der bald zur Überschreitung der Eingriffs- oder Warngrenze führt.

Ein „Muster“ ist ein nicht zufälliger Kurvenverlauf, z. B. ein periodisches „Schwingen“ um die Mittelwertlinie. Es kann sich dabei um Temperaturschwankungen handeln, die in der Produktion mal zu größeren, mal zu kleineren Teilen führen.

Ein Excel Vorlage zur Prozessstabilität hilft bei der Bestimmung dieser Schwankungen.

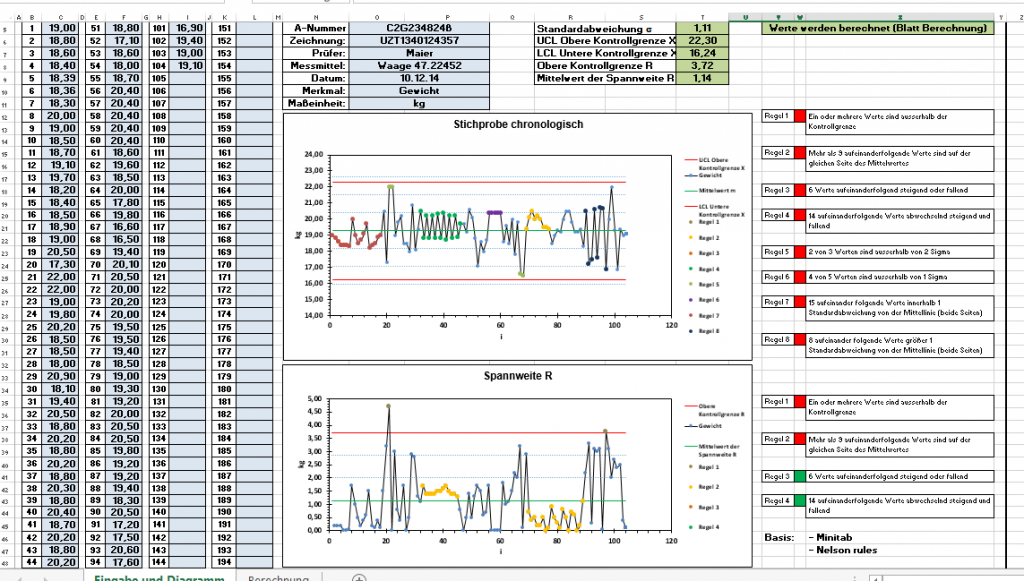
Man spricht von einem Durchlauf (oder „Run“), wenn 7 eingezeichnete Punkte über oder unter der Mittelwertlinie liegen. In diesem Fall hat sich der Prozessmittelwert wahrscheinlich verschoben. Dies kann z. B. darauf hindeuten, dass eine Werkzeugschneide beschädigt wurde und nun größere oder kleinere Teile herstellt.

Die Eingriffsgrenzen sind also nicht die einzigen Hinweise auf mögliche Probleme, auch die Anordnung der Messpunkte ist zu beachten. Liegen mehr als 90 % der Messpunkte im mittleren Drittel des Bereichs zwischen den Eingriffsgrenzen oder weniger als 40 % der Messpunkte in diesem Drittel, so ist ebenfalls von einem systematischen (nicht zufälligen) Einfluss auszugehen.

Weitere wichtige Inhalte für Ihr Projekt!

Folgen Sie den einzelnen, unten stehenden Links und Sie gelangen zum Thema und den entsprechenden Excel Dateien. Das Bild mit allen Links zu den Themen können Sie als pdf (Werkzeuge_20150722_4_als_pdf) downloaden.
Die Excel Vorlagen für die Lean Tools laden Sie in dieser Excel Datei (Toolbox.xlsx) runter.
Das Komplettpaket Excel Vorlagen Messsystemanalyse und Prozessfähigkeit finden Sie in dieser zip (Alle Vorlagen Messsystemanalyse_und_Prozessfähigkeit.zip) Datei.

Organisieren – Define Phase

• Projektauftrag
• Wasserfall Diagramm
• Stichprobe berechnen
• Business Case
• Pareto Prinzipg 80/20 Regel
• Z Wert Tabelle
• Change Management

Messen – Measure Phase

• Pareto Diagramm
• Konfidenzintervall
• Six Sigma Organisation
• Boxplot Diagramm
• Ursache Wirkungs Diagramm
• Smart Regel
• Qualitäts Kennzahlen
• Ishikawa Diagramm
• Projektabgrenzung
• Prozesskennzahlen
• Zeitanalyse
• Kick off
• OEE Gesamtanlagen- effektivität
• Sipoc

Analysieren – Measure Phase

• Messsystemanalyse Verfahren 1
• Messsystemanalyse Verfahren 2
• Messsystem fähig?
• Messsystem Analyse Verfahren 3
• Projektplan
• Messwert normalverteilt Anderson Darling
• Wahrscheinlichkeitsnetz
• Prozess / Maschine fähig? cp / cpk ausreichend?
• SPC Statistische Prozesskontrolle

Verbessern – Improve Phase

• 7 Arten der Verschwendung
• Paarweiser Vergleich Nutzwert Analyse
• Spaghetti Diagramm
• 5S Methode
• EPEI Every part every interval
• Wertstromanalyse Symbole
• Little’s Law
• Yamazumi chart Yamazumi board
• Wertstromanalyse
• 10er Regel der Fehlerkosten

Weiterbildung

• Green Belt
• Black Belt
• Black Belt Zertifizierung

Excel Funktionen

• Excel dynamisches Diagramm
• Zeichnen in Excel
• process capability