Die Berechnung der Maschinenfähigkeit ist abhängig von der Verteilung der Daten.
Als Standardmethode zur Berechnung der Fähigkeitskennwerte wird die Quantilmethode eingesetzt. Dies ist eine Methode, die für alle Verteilungsmodelle ohne Einschränkung verwendbar ist.
Für die Normalverteilung und Betragsverteilung 1. Art, kann die untenstehende Excel Vorlage verwendet werden.
Die Vorlage enthält:
- die Berechnung der Normalverteilung (Gewicht, Länge, etc…) incl. einseitiger Toleranzgrenzen
- die Berechnung der Betragsverteilung 1. Art (Rauheit, Rundheit, Rundlauf……) incl. natürlicher Toleranzgrenzen
- mehrere Sprachen (deutsch, englisch, italienisch, andere Sprachen auf Anfrage)
- etc.
Weitere Informationen und Excel Vorlagen finden Sie unter dem Beitrag Berechnung der Maschinen- und Prozessfähigkeit auf unserer Seite.
Benötigen Sie eine Implementierung der Betragsverteilung 1. Art in Ihrem Excel Template, schreiben Sie einfach eine Mail an roland.schnurr@sixsigmablackbelt.de.
Normalverteilung (N)
Die Normal- oder Gauß-Verteilung (nach Carl Friedrich Gauß) ist in der Stochastik ein wichtiger Typ stetiger Wahrscheinlichkeitsverteilungen. Ihre Wahrscheinlichkeitsdichtefunktion wird auch Gauß-Funktion, gaußsche Normalverteilung, gaußsche Verteilungskurve, Gauß-Kurve, gaußsche Glockenkurve, gaußsche Glockenfunktion, Gauß-Glocke oder schlicht Glockenkurve genannt.
Betragsverteilung 1. Art (B1)
Eine Betragsverteilung 1. Art entsteht durch Falten der Normalverteilung an einem beliebigen Punkt unterhalb des Erwartungswertes µ.
Durch die Faltung werden die Werte links von µ den Werten rechts von µ zugeschlagen. Diese Verteilungsform beschreibt im Allgemeinen eindimensionale, nullbegrenzte Merkmale mit Zielwert null wie Ebenheit, Rundheit, Parallelität usw.
Betragsverteilung 2. Art (B2)
In der Wahrscheinlichkeitstheorie und Statistik wird mit Rayleigh-Verteilung (nach John William Strutt, 3. Baron Rayleigh) oder Betragsverteilung 2. Art eine kontinuierliche Wahrscheinlichkeitsverteilung bezeichnet.
Wenn die Komponenten eines zweidimensionalen Zufallsvektors normalverteilt und stochastisch unabhängig sind, dann ist der Betrag Rayleigh-verteilt.
Typischerweise findet die Betragsverteilung 2. Art bei der Bewertung folgender Merkmale Verwendung: Position, Koaxialität, Rundlauf.
Übersicht Form und Lagetoleranzen incl. anzuwendender Verteilung
| Bezeichnung | Symbol | Ver-teilung | Definition |
| Gewicht | N | ||
| Länge | N | ||
| Rauheit | B1 | ||
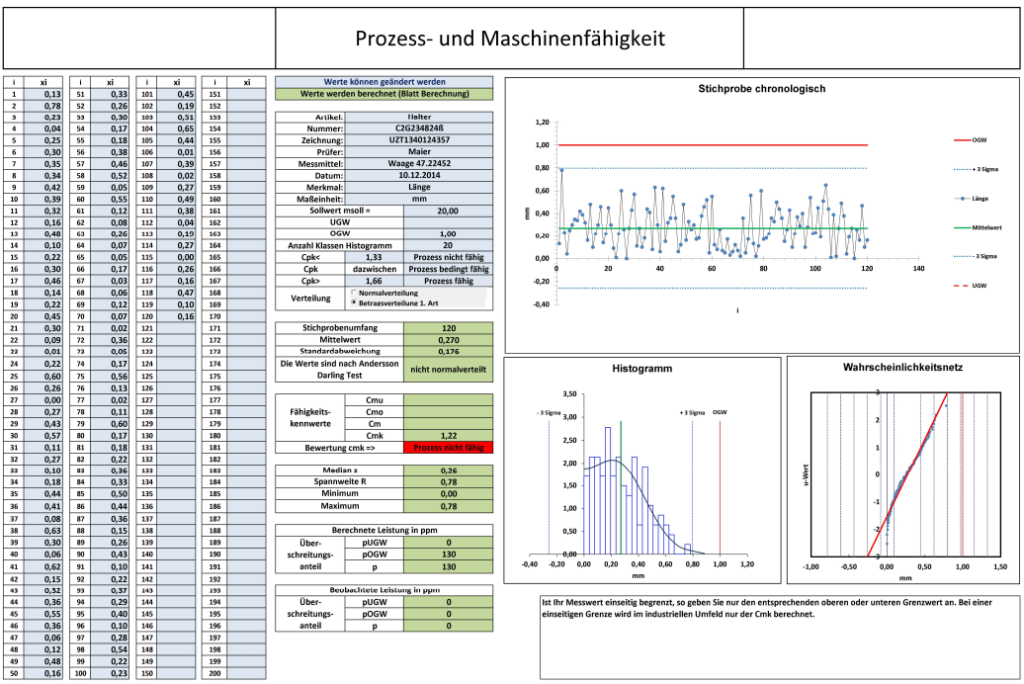
| Geradheit | 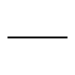 | B1 | für Flächen: Die tolerierte Linie muss in jeder Ebene zwischen zwei parallelen Geraden mit Abstand t liegen.[Anm. 1] für Achsen: Die tolerierte Achse muss in einem Zylinder (Ø = t) liegen. |
| Ebenheit |  | B1 | Die tolerierte Fläche muss zwischen zwei parallelen Ebenen (Abstand t) liegen. |
| Rundheit |  | B1 | Die tolerierte Umfangslinie muss in allen Schnittebenen senkrecht zur Mittelachse zwischen zwei konzentrischen Kreisen (Δr = t) liegen. |
| Profil einer Linie |  | B1 | Das tolerierte Profil muss in jeder Ebene zwischen zwei äquidistanten Hülllinien liegen, deren Abstand von Kreisen (Ø = t) definiert wird.[Anm. 2] |
| Profile einer Fläche | 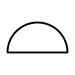 | B1 | Die tolerierte Fläche muss zwischen zwei äquidistanten Hüllflächen liegen, deren Abstand durch Kugeln (Ø = t) definiert wird.[Anm. 2] |
| Parallelität |  | B1 | für Flächen: Die tolerierte Fläche muss zwischen zwei Ebenen (Abstand t), welche parallel zum Bezug sind, liegen. für Achsen: Die tolerierte Achse muss in einem Zylinder (Ø = t), dessen Achse parallel zum Bezug ist, liegen. |
| Rechtwinkligkeit | 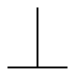 | B1 | für Flächen: Die tolerierte Fläche muss zwischen zwei Ebenen (Abstand t), welche senkrecht zum Bezug sind, liegen.für Achsen: Die tolerierte Zylinderachse muss in einem zur Bezugsfläche senkrechten Zylinder (Ø = t) liegen. |
| Winkligkeit | 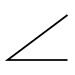 | B1 | für Flächen: Die tolerierte Fläche muss zwischen zwei Ebenen (Abstand t), welche im angegebenen Winkel zum Bezug geneigt sind, liegen. für Achsen: Die tolerierte Achse muss zwischen zwei parallelen Ebenen (Abstand t), welche im angegebenen Winkel zum Bezug geneigt sind, liegen. |
| Position | 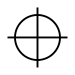 | B2 | Der Bohrungsmittelpunkt muss in einem Quadrat (a = t), dessen Mittelpunkt mit der theoretisch genauen Position der Bohrung übereinstimmt, liegen.[Anm. 3]mit Ø-Zeichen: Der Bohrungsmittelpunkt muss in einem Kreis (Ø = t), dessen Mittelpunkt mit der theoretisch genauen Position der Bohrung übereinstimmt, liegen.[Anm. 4] Ebenfalls kann die Position von Flächen definiert werden. |
| Konzentrizität Koaxialität |  | B2 | Der Mittelpunkt des tolerierten Kreises muss in einem Kreis (Ø = t), dessen Mittelpunkt konzentrisch zum Bezug ist, liegen.[Anm. 5]Die Achse der tolerierten Fläche muss in einem Zylinder (Ø = t), dessen Mittelachse koaxial zum Bezug ist, liegen.[Anm. 5] |
| Symmetrie | 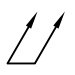 | B1 | Die tolerierte Mittelebene muss zwischen zwei parallelen Ebenen (Abstand t), welche symmetrisch zum Bezug sind, liegen. |
| Rundlauf (radial) Planlauf (axial |  | B1 / B2 | Bei einer Umdrehung um die Bezugsachse darf die Rundlaufabweichung t nicht überschreiten.Bei einer Umdrehung um die Bezugsachse darf die Planlaufabweichung t nicht überschreiten. |