Eine Regelkarte ist ein Diagramm zur grafischen Darstellung von statistischen Kennwerten. Als zentrales Werkzeug der statistischen Prozesskontrolle (SPC) beinhaltet eine Mittellinie und Kontrollgrenzen. Die Mittellinie wird über den Mittelwert ermittelt. Die Kontrollgrenzen, auch Eingriffsgrenzen genannt, berechnen sich mithilfe der Standardabweichung.
Wie erkennt man, ob ein Produktionsprozess stabil läuft oder ob Abweichungen nur zufällig sind? Genau hier kommt die Qualitätsregelkarte (QRK) ins Spiel, ein zentrales Werkzeug der Statistischen Prozesskontrolle (SPC).
Das Herzstück jeder Regelkarte sind die Eingriffsgrenzen (obere und untere Eingriffsgrenze, OEG/UEG). Sie fungieren als statistische Leitplanken für Ihren Prozess. Solange sich die Messwerte innerhalb dieser Grenzen bewegen, ist alles im grünen Bereich. Überschreitet ein Wert eine Grenze, ist das ein klares Signal zum Handeln.
In diesem Artikel lernen Sie:
- Warum Eingriffsgrenzen entscheidend für die Prozesssteuerung sind.
- Wie Sie die Eingriffsgrenzen für eine X-quer-Regelkarte Schritt für Schritt berechnen.
- Wie Sie unsere kostenlose Excel-Vorlage für eine schnelle Analyse nutzen.
Wollen Sie die einfach nur die Berechnung umsetzen, nutzen Sie unsere kostenlose Excel Vorlage, die Teil unseres Komplettpaketes ist.

Warum sind Eingriffsgrenzen so wichtig?
Eingriffsgrenzen basieren nicht auf Toleranzvorgaben des Kunden, sondern ausschließlich auf der natürlichen Streuung Ihres Prozesses. Ihre Hauptaufgabe ist es, zwei Arten von Ursachen für Prozessschwankungen zu unterscheiden:
- Zufällige Ursachen (Common Causes): Das normale „Grundrauschen“ eines jeden stabilen Prozesses. Diese Schwankungen sind unvermeidbar und vorhersehbar.
- Systematische oder Besondere Ursachen (Special Causes): Unvorhergesehene Ereignisse, die den Prozess aus dem Ruder laufen lassen (z. B. ein Werkzeugverschleiß, Materialfehler, falsche Einstellung).
Die Eingriffsgrenzen helfen Ihnen, systematische Ursachen sofort zu identifizieren. Somit können Sie gegensteuern, bevor Ausschuss produziert wird.
Berechnung der Eingriffsgrenzen: Eine Schritt-für-Schritt-Anleitung
Wir konzentrieren uns auf die Berechnung für eine X-quer-Regelkarte, eine der am häufigsten verwendeten Regelkarten.
Die Aufgabe von Regelkarten ist es, den Mittelwert und die Standardabweichung eines Prozesses abzuschätzen. Der Mittelwert ist leicht zu berechnen und zu verstehen. Der Mittelwirt ist einfach der Durchschnitt aller Ergebnisse. Die Standardabweichung ist etwas schwieriger zu verstehen. Es gibt mehrere Möglichkeiten die Standardabweichung zu berechnen. Je nach Berechnung der Standardabweichung ergeben sich unterschiedliche Kontrollgrenzen.
Untergruppen der Werte
Für unsere Beispielrechnung nutzen wir die folgenden Daten aus 10 Untergruppen mit je 3 Messwerten:
| Untergruppe | X1 | X2 | X3 | Untergruppe Durchschnitt | Untergruppe R | Untergruppe s |
| 1 | 74,0300 | 74,0020 | 74,0190 | 74,0170 | 0,0280 | |
| 2 | 73,9950 | 73,9920 | 74,0010 | 73,9960 | 0,0090 | |
| 3 | 73,9880 | 74,0240 | 74,0210 | 74,0110 | 0,0360 | |
| 4 | 74,0020 | 73,9960 | 73,9930 | 73,9970 | 0,0090 | |
| 5 | 73,9920 | 74,0070 | 74,0150 | 74,0047 | 0,0230 | |
| 6 | 74,0090 | 73,9940 | 73,9970 | 74,0000 | 0,0150 | |
| 7 | 73,9950 | 74,0060 | 73,9940 | 73,9983 | 0,0120 | |
| 8 | 73,9850 | 74,0030 | 73,9930 | 73,9937 | 0,0180 | |
| 9 | 74,0080 | 73,9950 | 74,0090 | 74,0040 | 0,0140 | |
| 10 | 73,9980 | 74,0000 | 73,9900 | 73,9960 | 0,0100 | |
| Summe | 740,0177 | 0,1740 | ||||
| Durchschnitt | 74,0018 | 0,0174 |
Die Untergruppengröße ist für jede der 10 Untergruppen konstant. Der Untergruppendurchschnitt, die Spannweite und die Standardabweichung wurden ebenfalls für die unten stehende Verwendung berechnet. Die Gesamtsumme und der Gesamtdurchschnitt werden für die Untergruppendurchschnitte, die Untergruppen – Spannweiten und die Untergruppen-Standardabweichungen angegeben. Aufgrund von Rundungen kann es zu geringfügigen Abweichungen kommen.
Möglichkeiten zur Schätzung der Standardabweichung
Wir werden uns drei verschiedene Möglichkeiten zur Schätzung der Standardabweichung ansehen. Diese wirken sich darauf aus, wie die Kontrollgrenzen berechnet werden. Die Kontrollgrenzen für die X-Karte sind gegeben durch:
Kontrollgrenzen basierend auf Sigma
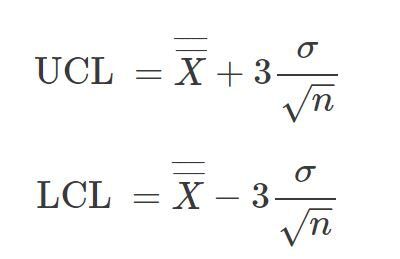
wobei UCL und LCL die obere und untere Kontrollgrenze, n die Untergruppengröße und σ die geschätzte Standardabweichung der einzelnen Werte ist. Zur Erinnerung: Die Standardabweichung der Untergruppenmittelwerte ist gleich der Standardabweichung der Einzelwerte geteilt durch die Quadratwurzel der Untergruppengröße. Diese Gleichungen zur Berechnung der Kontrollgrenzen können sich von den von Ihnen normalerweise verwendeten Gleichungen unterscheiden.
Der Wert von σ hängt von der Methode ab, die Sie zu seiner Schätzung verwenden. Wir werden uns drei Methoden zur Schätzung von σ für Untergruppendaten ansehen:
- Durchschnitt der Untergruppenbereiche
- Durchschnitt der Standardabweichungen der Untergruppe
- Gepoolte Standardabweichung
A. Durchschnitt der Untergruppenbereiche
Der Mittelwert der Untergruppenbereiche ist die klassische Methode zur Schätzung der Standardabweichung. Der Durchschnittsbereich ist einfach der Durchschnitt der Subgruppen-Durchschnitte, wenn die Subgruppengröße konstant ist:
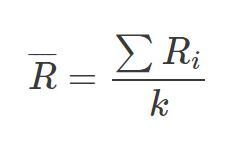
wobei Ri der Bereich der i-ten Untergruppe und k die Anzahl der Untergruppen ist. Die Standardabweichung wird dann anhand der folgenden Gleichung geschätzt:
und Sigma
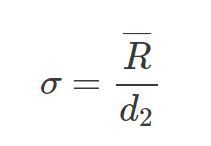
wobei d2 eine Konstante ist, die von der Größe der Untergruppe abhängt.
Tabelle 2 zeigt die Werte von d2 basierend auf Subgruppengrößen bis zu 10. Aus der Tabelle können Sie ersehen, dass d2 für eine Subgruppengröße von 3 1,693 beträgt.
| n | d2 | c4 |
| 2 | 1,128 | 0,7979 |
| 3 | 1,693 | 0,8862 |
| 4 | 2,059 | 0,9213 |
| 5 | 2,326 | 0,9400 |
| 6 | 2,534 | 0,9515 |
| 7 | 2,704 | 0,9594 |
| 8 | 2,847 | 0,9650 |
| 9 | 2,970 | 0,9693 |
| 10 | 3,078 | 0,9727 |
Anhand der Schätzung der Standardabweichung vom Mittelwertbereich berechnen wir die Kontrollgrenzen mit folgender Formel:
Für die obere Kontrollgrenze
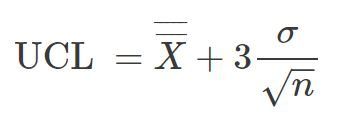
Für die untere Kontrollgrenze
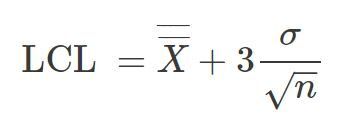
Für obiges Beispiel:
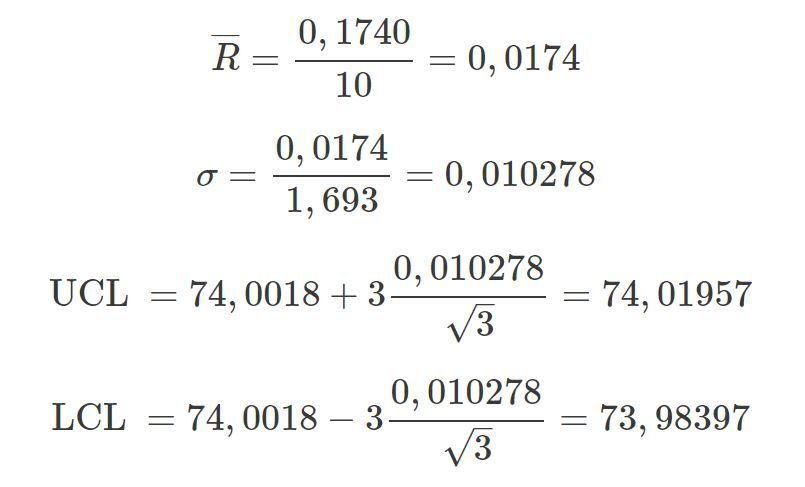
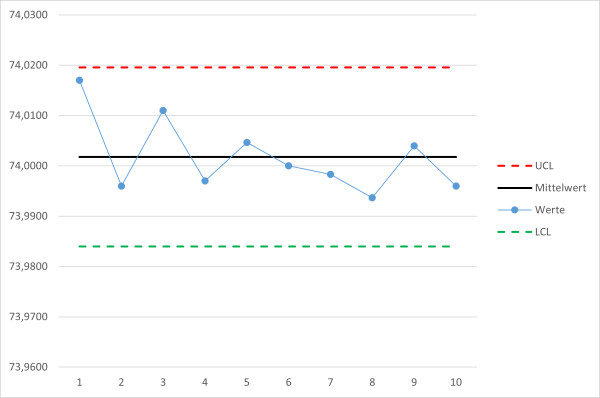
Praktische Umsetzung mit unserer Excel-Vorlage
Die manuelle Berechnung ist für das Verständnis wichtig, in der Praxis aber zeitaufwändig. Nutzen Sie unsere praxiserprobte Excel-Vorlage, um Ihre Daten schnell und fehlerfrei auszuwerten.
Wollen Sie die Berechnung Excel überlassen erfahren Sie hier mehr zur Regelkarte incl. einer entsprechenden Excel Vorlage.
(Hinweis: Die Vorlage ist Teil des umfassenden MSA / Prozessfähigkeits – Pakets)
Weitere wichtige Inhalte für Ihr Projekt!
Folgen Sie den einzelnen, unten stehenden Links und Sie gelangen zum Thema und den entsprechenden Excel Dateien. Das Bild mit allen Links zu den Themen können Sie als pdf (Werkzeuge_20150722_4_als_pdf) downloaden.
Die Excel Vorlagen für die Lean Tools laden Sie in dieser Excel Datei (Toolbox.xlsx) runter.
Das Komplettpaket Excel Vorlagen Messsystemanalyse und Prozessfähigkeit können Sie hier anfordern.
Organisieren – Define Phase
Messen – Measure Phase
- Pareto Diagramm
- Konfidenzintervall
- Boxplot Diagramm
- Ursache Wirkungs Diagramm
- Qualitäts Kennzahlen
- Ishikawa Diagramm
- Prozesskennzahlen
- Kick off
- Sipoc