Median Excel Mittelwert

Der Mittelwert als Median und arithmetischer Mittelwert findet auch unter den Bezeichnungen Mittel oder Durchschnitt Verwendung.

Wollt ihr Zeit und Arbeit sparen tragt eure Werte in die Median Mittelwert.xls Excel Tabelle ein. Die Tabelle errechnet die Werte automatisch.

Allgemein kann man den Mittelwert berechnen, indem man aus der Summe von zwei Zahlen eine weitere berechnet, die zwischen den Zahlen liegt.

Dies kann nach unterschiedlichen Vorgehensweisen geschehen. In diesem Beitrag sollen die Unterschiede zwischen dem arithmetischen Mittelwert und dem Median erläutert werden. Nach dem Lesen des Beitrages werdet Ihr verstehen, warum der arithmetische Mittelwert und der Median immer in Kombination betrachtet werden sollten. Im Übrigen gilt: der Mittelwert und auch der Median sind wichtige Kennzahlen zur Beurteilung von Werten einer Beobachtung.

Inhalte Verbergen

1 Mittelwert (arithmetischer Mittelwert)

1.1 Mittelwert Definition

1.2 Mittelwert berechnen Formel

1.3 Beispiel Mittelwert berechnen

1.4 Mittelwert berechnen mit Excel

1.5 Warum sollte man den Mittelwert immer in Verbindung mit dem Median betrachten?

2 Median

2.1 Median Definition

2.2 Geordneter Datensatz Definition

2.3 Berechnung Median

2.4 Median berechnen online

3 Median Mittelwert Vergleich

Mittelwert (arithmetischer Mittelwert)

Mittelwert Definition

Der Mittelwert im klassischen Sinne wird als arithmetischer Mittelwert beschrieben. Das arithmetische Mittel ergibt sich aus der Summe aller Beobachtungwerte geteilt durch die Anzahl der Beobachtungswerte.

Mittelwert berechnen Formel

Die mathematische Formel zur Mittelwert Berechnung lautet:

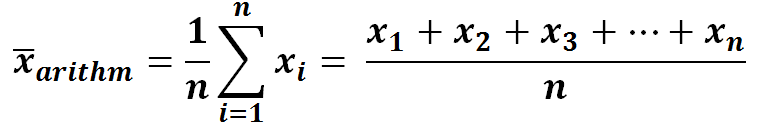
Beispiel Mittelwert berechnen

Der Mittelwert wird oft benutzt um allgemein gültige Aussagen zu einem Sachverhalt zu machen. Bei unten dargestellten Beispiel könnte die Fragestellung lauten: „Was verdienen die Mitarbeiter in der Abteilung Rechnungswesen im Durchschnitt?“. Im Einzelnen erhalten die Mitarbeiter der Abteilung folgendes Gehalt in €.

Maier	2500
Huber	2000
Müller	2300
Volz	6500
Gerber	2700
Weber	2600
Bauer	2650
Gauck	2700

Nach unserer Formel bedeutet dies:
Summe der Gehälter=2.500+2.000+2.300+6.500+2.700+2.600+2.650+2.700=23.950
Anzahl der Werte = 8
Arithmetischer Mittelwert= 23.950 / 8 = 2.993,75

Wir würden nun darauf schließen, dass im umgangssprachlichen Mittel alle Mitarbeiter ca. 3.000 € verdienen. Tatsächlich ist es aber so, dass 7 Mitarbeiter deutlich weniger als 3.000 € verdienen. Ein Mitarbeiter aber sogar mehr als das Doppelte von 3.000 € verdient. Die Aussagekraft des arithmetischen Mittelwertes sollte also durch eine zweite Kennzahl ergänzt werden. Dies ist der Median.

Mittelwert berechnen mit Excel

In Excel gibt es verschiedene Möglichkeiten mit denen wir den Mittelwert berechnen:

Mit der Funktion Summe (Formeln ->Summe) können wir die Summe der Gehälter berechnen
Mit der Funktion Anzahl (Formeln -> Anzahl) können wir die Anzahl der Gehälter berechnen.
Anschließend wird die Summe der Gehälter durch die Anzahl der Gehälter geteilt

Als Alternative lässt sich der arithmetische Mittelwert mit der Funktion Mittelwert (Formeln -> Mittelwert) direkt in Excel berechnen.

Warum sollte man den Mittelwert immer in Verbindung mit dem Median betrachten?

Der Mittelwert ist bei wenigen Daten sehr empfindlich gegenüber Ausreißern. Ausreißer sind ungewöhnliche Beobachtungswerte, die sich außerhalb der normalen Beobachtung bewegen. Hier hilft der Median zur richtigen Interpretation der Werte. Wie ihr in obigem Beispiel gesehen habt, kann ein Ausreißer die Interpretation des Ergebnisses in sehr großem Maße beeinflussen. Der arithmetische Mittelwert hat darüberhinaus einen zweiten Nachteil. Bei unsymetrischen Datensätzen repräsentiert er nicht unbedingt die Lage der Mehrheit der Daten. Diese Nachteile gleicht der Median aus. Der Median gilt daher als „robuste“ Kennzahl.

Median

Median Definition

Der Median ist der Wert in der Mitte eines der Größe nach geordneten Datensatzes. Er teilt die Anzahl der Werte in zwei gleich große Hälften. Als ersten Schritt bei der Berechnung des Medians werden die ungeordneten Daten in geordnete Daten überführt.

Geordneter Datensatz Definition

Ein ungeordneter Datensatz wird mit x₁, x₂, x₃,… bezeichnet. 1,2,3,… bezeichnen hierbei die Reihenfolge der Erhebung. Sortiert man die Werte zur Berechnung des Medians nun der Größe nach aufsteigend, so werden die Werte mit x₍₁₎, x₍₂₎, x₍₃₎ bezeichnet.
Folgende Daten (ungeordnet) aus dem obigen Beispiel:
x₁=2.500, x₂=2.000, x₃=2.300, x₄=6.500

Dies ergibt folgende Daten (geordnet) aus dem obigen Beispiel:
x₍₁₎=2.000, x₍₂₎=2.300, x₍₃₎=2.500, x₍₄₎=6.500

Berechnung Median

Für die Berechnung des Medians sind zwei Möglichkeiten vorhanden, je nachdem ob eine gerade Zahl oder eine ungerade Zahl von Werten vorliegt.

Median berechnen gerade Zahl

Bei einer geraden Anzahl von Werten (n) entspricht der Median dem Mittelwert der beiden mittleren Werten. Die mathematische Median Formel lautet hierzu:

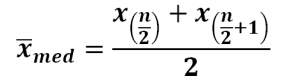
Anbei ein Beispiel Median berechnen gerade Zahl:

Daten (geordnet) aus dem obigen Beispiel:
x₍₁₎=2.000, x₍₂₎=2.300, x₍₃₎=2.500, x₍₄₎=6.500
n=4
Median = (x₍₂₎ + x₍₃₎)/2= (2.300+2.500)/2 = 2.400

Median berechnen ungerade Zahl

Bei einer ungeraden Anzahl von Werten (n) entspricht der Median dem mittleren Wert. Die mathematische Formel hierzu lautet.

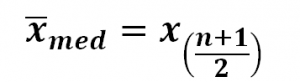
Beispiel Median berechnen

Wir nehmen den fünften Wert des ursprünglichen Beispiels hinzu (x₅=2.700). Es ergeben sich folgende geordnete Daten:
x₍₁₎=2.000, x₍₂₎=2.300, x₍₃₎=2.500, x₍₄₎=2.700, x₍₅₎=6.500
n=5
Median= x_((5+1)/2)=x₍₃₎=2.500

Median Excel Berechnung

In Excel gibt es verschiedene Möglichkeiten mit denen wir den Median berechnen können.

Etwas aufwändig ist die Möglichkeit die Daten mit der Sortierfunktion von Excel in einen geordneten Datensatz zu überführen. Anschließend werden die oben genannten Regeln für gerade und ungerade Anzahl von Werten angewendet.

Einfacher ist die Funktion Median (Formeln->Median) zu verwenden. Man erhält somit automatisch den Median der Datenreihe, ohne diese vorher sortieren zu müssen

Median berechnen online

Ihr könnt die Werte für den arithmetischen Mittelwert oder den Median auch online berechnen. Hierzu fügt Ihr Eure vorhandenen Werte in die Tabelle unter folgendem Link im Reiter „Mittelwert Median“ ein. Ihr erhaltet dann automatisch die berechneten Werte.

Median Mittelwert Vergleich

Als Ergänzung noch einmal Median und Mittelwert für die ursprüngliche Fragestellung

„Was verdienen die Mitarbeiter in Abteilung Rechnungswesen im Durchschnitt?“.

Maier	2500
Huber	2000
Müller	2300
Volz	6500
Gerber	2700
Weber	2600
Bauer	2650
Gauck	2700

Wie oben berechnet war das arithmetische Mittel = 2.993,75

Wie ist nun der Median im Vergleich?

Wir ordnen den Datensatz
x₍₁₎=2.000, x₍₂₎=2.300, x₍₃₎=2.500, x₍₄₎=2.600, x₍₅₎=2.650, x₍₆₎=2.700, x₍₇₎=2.700, x₍₈₎=6.500
n=8
Median = (x₍₄₎ + x₍₅₎)/2= (2.600+2.650)/2 = 2.625

Dies bedeutet 50% der Personen verdienen gleich oder weniger als 2.625 €.
Dies bedeutet 50% der Personen verdienen gleich oder mehr als 2.625 €.

Wenn ihr nun die Werte 2.993 und 2.625 vergleicht, seht ihr welchen Unterschied arithmetischer Mittelwert und Median bilden. Der Median ist der robustere Wert und sagt meiner Meinung nach mehr aus. Jede Diskussion zu meiner Ansicht, stehe ich auch hier offen gegenüber.

Weitere wichtige Inhalte für Ihr Projekt!

Folgen Sie den einzelnen, unten stehenden Links und Sie gelangen zum Thema und den entsprechenden Excel Dateien. Das Bild mit allen Links zu den Themen können Sie als pdf (Werkzeuge_20150722_4_als_pdf) downloaden.
Die Excel Vorlagen für die Lean Tools laden Sie in dieser Excel Datei (Toolbox.xlsx) runter.
Das Komplettpaket Excel Vorlagen Messsystemanalyse und Prozessfähigkeit können Sie hier anfordern.